Question

（2013•嘉兴一模）已知椭圆C₁：

x2

16

+

y2

15

=1的左焦点为F，点P为椭圆上一动点，过点以F为圆心，1为半径的圆作切线PM，PN，其中切点为M，N则四边形PMFN面积的最大值 为

2

6

．

Answer 1

分析：连接PF，根据圆的切线的性质得S_△AFM=

1

2

|PM|•|MF|=

1

2

|PM|，从而四边形PMFN面积S=2S_△AFM=|PM|．根据勾股定理，得|PM|=

|PF|2-1

，因此当|PF|最长时|PM|达到最大值．再根据椭圆的几何性质，得P与椭圆右顶点重合时，|PF|最长，由此可得|PM|最大值为2

6

，即得四边形PMFN面积的最大值．

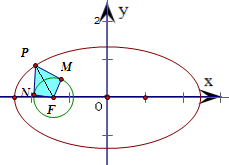解答：解：连接PF，
∵PM与圆F相切，∴PM⊥MF，可得S_△AFM=

1

2

|PM|•|MF|=

1

2

|PM|
根据对称性可得四边形PMFN面积S=2S_△AFM=|PM|
Rt△PMF中，|PM|=

|PF|2-|MF|2

=

|PF|2-1

因此，当|PF|最长时，|PM|达到最大值，
同时四边形PMFN面积S达最大值．
由椭圆的几何性质，得
当P与椭圆

x2

16

+

y2

15

=1右顶点（4，0）重合时，|PF|最长．
∵左焦点F坐标为（-1，0），
∴|PF|最大值为|4-（-1）|=5，可得|PM|最大值为

52-1

=2

6

可得四边形PMFN面积S的最大值为2

6

故答案为：2

6

点评：本题给出椭圆内有一个内含于椭圆的小圆，求椭圆上一点P切圆的两条切线和过切点两条半径构成的四边形面积的最大值，着重考查了椭圆的几何性质、勾股定理和直线与圆的位置关系等知识，属于中档题．