题目内容
（2013•嘉兴一模）如图，直角梯形ABCD中，AB∥CD，∠BCD=90°，BC=CD=| 2 |
（Ⅰ）求证：AD丄BF；
（Ⅱ）若线段EC的中点为M，求直线AM与平面ABEF所成角的正弦值．
分析：（I）梯形ABCD中，根据勾股定理和等腰三角形的判定，可得∠ADB=90°即AD⊥BD，结合AD⊥DF利用线面垂直的判定定理，证出AD⊥平面BDF，进而可得AD丄BF；
（II）过点M作MN⊥BE，垂足为N，连接NA，AC．利用线面垂直的判定与性质，证出MN⊥平面ABEF，从而得到∠MAN就是直线AM与平面ABEF所成角．Rt△BCE中利用相似算出MN=
，分别在Rt△ABC、Rt△ACM中运用勾股定理，算出AM=
．最后在Rt△MAN中利用正弦的定义，即可算出直线AM与平面ABEF所成角的正弦值等于
．
（II）过点M作MN⊥BE，垂足为N，连接NA，AC．利用线面垂直的判定与性质，证出MN⊥平面ABEF，从而得到∠MAN就是直线AM与平面ABEF所成角．Rt△BCE中利用相似算出MN=
| ||
| 3 |
| 11 |
| ||
| 33 |
解答：解：（I）∵BC⊥DC，BC=CD=
，
∴BD=
=2，且△BCD是等腰直角三角形，∠CDB=∠CBD=45°
∵平面ABCD中，AB∥DC，∴∠DBA=∠CBD=45°
∵AD=BD，可得∠DBA=∠BAD=45°
∴∠ADB=90°，即AD⊥BD
∵FD丄底面ABCD，AD?底面ABCD，∴AD⊥DF
∵BD、DF是平面BDF内的相交直线，∴AD⊥平面BDF
∵BF?平面BDF，∴AD丄BF
（II）如图，过点M作MN⊥BE，垂足为N，连接NA，AC
∵AB⊥BC，AB⊥EC，BC∩EC=E，∴AB⊥平面BEC
∵MN?平面BEC，∴AB⊥MN，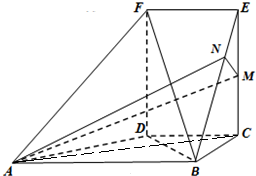
结合MN⊥BE且BE∩AB=B，可得MN⊥平面ABEF
∴AN是AM在平面ABEF内的射影，可得∠MAN就是直线AM与平面ABEF所成角
∵Rt△ABC中，AC=
=
，∴Rt△ACM中，AM=
=
．
∵△EMN∽△EBC，∴
=
=
，可得MN=
因此，在Rt△MAN中，sin∠MAN=
=
即直线AM与平面ABEF所成角的正弦值是
．
| 2 |
∴BD=
| BC2+CD2 |
∵平面ABCD中，AB∥DC，∴∠DBA=∠CBD=45°
∵AD=BD，可得∠DBA=∠BAD=45°
∴∠ADB=90°，即AD⊥BD
∵FD丄底面ABCD，AD?底面ABCD，∴AD⊥DF
∵BD、DF是平面BDF内的相交直线，∴AD⊥平面BDF
∵BF?平面BDF，∴AD丄BF
（II）如图，过点M作MN⊥BE，垂足为N，连接NA，AC
∵AB⊥BC，AB⊥EC，BC∩EC=E，∴AB⊥平面BEC
∵MN?平面BEC，∴AB⊥MN，
结合MN⊥BE且BE∩AB=B，可得MN⊥平面ABEF
∴AN是AM在平面ABEF内的射影，可得∠MAN就是直线AM与平面ABEF所成角
∵Rt△ABC中，AC=
| AB2+BC2 |
| 10 |
| AC2+CM2 |
| 11 |
∵△EMN∽△EBC，∴
| MN |
| BC |
| EN |
| EC |
| MN |
| BC |
| EM |
| EB |
| ||
| 3 |
因此，在Rt△MAN中，sin∠MAN=
| MN |
| AM |
| ||
| 33 |
即直线AM与平面ABEF所成角的正弦值是
| ||
| 33 |
点评：本题给出由四棱锥与三棱锥组合而成的几何体，求证线线垂直并求直线与平面所成角正弦值，着重考查了线面垂直的判定与性质和直线与平面所成角的求法等知识，属于中档题．．
练习册系列答案
寒假学与练系列答案
相关题目
（2013•嘉兴一模）一个几何体的三视图如图所示，则该几何体的体积为