题目内容
【题目】已知正方体ABCD﹣A1B1C1D1 ， O是底ABCD对角线的交点．求证：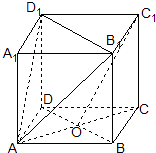 
（1）C1O∥面AB1D1；
（2）面BDC1∥面AB1D1 ．
【答案】
（1）证明：连接A1C1，设A1C1∩B1D1=O1
连接AO1，∵ABCD﹣A1B1C1D1是正方体
∴A1ACC1是平行四边形
∴A1C1∥AC且A1C1=AC
又O1，O分别是A1C1，AC的中点，
∴O1C1∥AO且O1C1=AO
∴AOC1O1是平行四边形
∴C1O∥AO1，AO1面AB1D1，C1O面AB1D1
∴C1O∥面AB1D1
（2）证明： 
是平行四边形，
∴ 
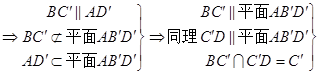平面C′DB∥平面AB′D′
【解析】（1）由题意连接A1C1 ， 先证明A1ACC1是平行四边形得A1C1∥AC且A1C1=AC，再证AOC1O1是平行四边形，然后利用直线与平面平行的判定定理进行证明；（2）因为AB∥CD∥D′C′，加上AB=CD=D′C′，可证ABC′D′是平行四边形，同理可证C′D∥平面AB′D′，从而求证．
【考点精析】根据题目的已知条件，利用直线与平面平行的判定和平面与平面平行的判定的相关知识可以得到问题的答案，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；判断两平面平行的方法有三种:用定义；判定定理；垂直于同一条直线的两个平面平行．
练习册系列答案
相关题目
