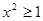题目内容
已知命题p:?x∈R,cos2x+sinx+a≥0,命题q:?x∈R,ax2-2x+a<0,命题p∨q为真,命题p∧q为假.求实数a的取值范围.
由命题p得a≥-cos2x-sinx=2sin2x-sinx-1=2(sinx-
)2-
,
因为sinx∈[-1,1],
所以当sinx=-1时,(2sin2x-sinx-1)max=2,
所以命题p:a≥2
由命题q得:当a≤0时显然成立;
当a>0时,需满足△=4-4a2>0,解得0<a<1
所以命题q:a<1
因为命题p∨q为真,命题p∧q为假,所以命题p和q一真一假
若命题p真q假,则a≥2;若命题p假q真,则a<1
综上,实数a的取值范围是(-∞,1)∪[2,+∞)
| 1 |
| 4 |
| 9 |
| 8 |
因为sinx∈[-1,1],
所以当sinx=-1时,(2sin2x-sinx-1)max=2,
所以命题p:a≥2
由命题q得:当a≤0时显然成立;
当a>0时,需满足△=4-4a2>0,解得0<a<1
所以命题q:a<1
因为命题p∨q为真,命题p∧q为假,所以命题p和q一真一假
若命题p真q假,则a≥2;若命题p假q真,则a<1
综上,实数a的取值范围是(-∞,1)∪[2,+∞)

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
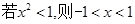 ”的逆否命题是( )
”的逆否命题是( )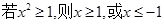
 ,则
,则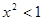
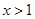 或
或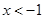 ,则
,则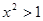
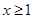 或
或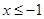 ,则
,则