题目内容
已知正数数列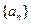
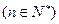 中,前
中,前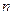 项和为
项和为 ,且
,且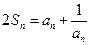 ,
,
用数学归纳法证明: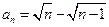 .
.
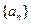
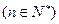 中,前
中,前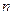 项和为
项和为 ,且
,且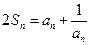 ,
,用数学归纳法证明:
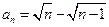 .
.同解析
(1)当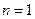 时.
时.
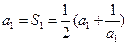 ,∴
,∴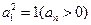 ,∴
,∴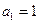 ,又
,又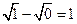 ,
,
∴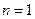 时,结论成立.
时,结论成立.
(2)假设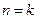 时,
时,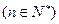 ,结论成立,即
,结论成立,即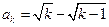 ,
,
当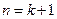 时,
时,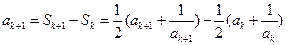 ,
,
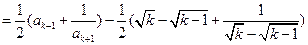
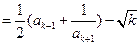
∴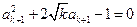 ,解得
,解得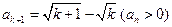 ,
,
∴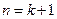 时,结论成立,
时,结论成立,
由(1)(2)可知,对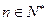 都有
都有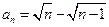
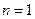 时.
时.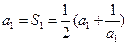 ,∴
,∴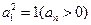 ,∴
,∴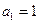 ,又
,又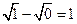 ,
,∴
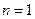 时,结论成立.
时,结论成立.(2)假设
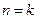 时,
时,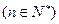 ,结论成立,即
,结论成立,即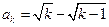 ,
,当
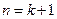 时,
时,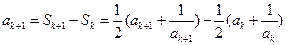 ,
,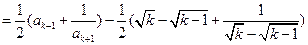
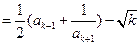
∴
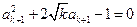 ,解得
,解得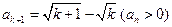 ,
,∴
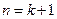 时,结论成立,
时,结论成立,由(1)(2)可知,对
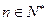 都有
都有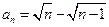

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
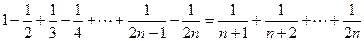
 ,
, ,
, ,且
,且 .求证:
.求证: .
.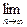 S2n<3,求q的取值范围
S2n<3,求q的取值范围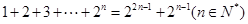 ,第二步,“假设当
,第二步,“假设当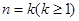 时等式成立,则当
时等式成立,则当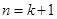 时有
时有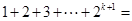
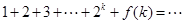 ”,其中
”,其中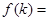 .
.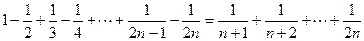
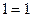 ,
,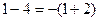 ,
,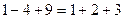 ,
,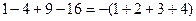 ,则第5个等式为 ,…,推广到第
,则第5个等式为 ,…,推广到第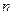 个等式为__ _;(注意:按规律写出等式的形式,不要求计算结果.)
个等式为__ _;(注意:按规律写出等式的形式,不要求计算结果.)