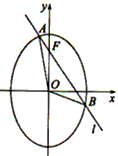
题目内容
已知O为坐标原点,F为抛物线y2=4x的焦点,A是抛物线上一点,若
•
=-4,则点A的坐标是
| OA |
| AF |
(1,2)或(1,-2)
(1,2)或(1,-2)
.分析:先求出抛物线的焦点F(1,0),根据抛物线的方程设A(
,y0),然后构成向量
、
,再由
•
=-4可求得y0的值,最后可得答案.
| ||
| 4 |
| OA |
| OB |
| OA |
| AF |
解答:解析∵抛物线的焦点为F(1,0),设A(
,y0),
则
=(
,y0),
=(1-
,-y0),
由
•
=-4,得y0=±2,
∴点A的坐标是(1,2)或(1,-2).
故答案为:(1,2)或(1,-2)
| ||
| 4 |
则
| OA |
| ||
| 4 |
| AF |
| ||
| 4 |
由
| OA |
| AF |
∴点A的坐标是(1,2)或(1,-2).
故答案为:(1,2)或(1,-2)
点评:本题主要考查抛物线的标准方程.抛物线的标准方程是高考的考点,是圆锥曲线的重要的一部分,要重视复习.

练习册系列答案
相关题目
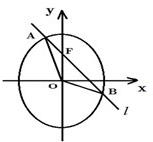 已知O为坐标原点,F为椭圆C:
已知O为坐标原点,F为椭圆C: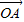 •
•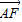 =-4,则点A的坐标是 .
=-4,则点A的坐标是 .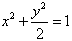 在y轴正半轴上的焦点,过F且斜率为
在y轴正半轴上的焦点,过F且斜率为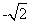 的直线l与C交于A、B两点,点P满足
的直线l与C交于A、B两点,点P满足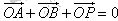 。
。