题目内容
已知函数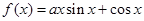 ,且
,且 在
在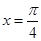 处的切线斜率为
处的切线斜率为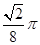 .
.
(1)求 的值,并讨论
的值,并讨论 在
在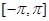 上的单调性;
上的单调性;
(2)设函数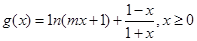 ,其中
,其中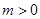 ,若对任意的
,若对任意的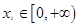 总存在
总存在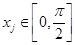 ,使得
,使得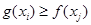 成立,求
成立,求 的取值范围.
的取值范围.
(Ⅰ)  在
在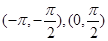 上单调递增,在
上单调递增,在  上单调递减
上单调递减
(Ⅱ) 
解析试题分析:(Ⅰ) 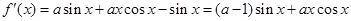
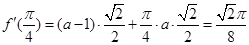
∴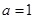 ∴
∴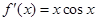
∴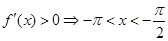 ,或
,或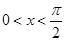
∴ ,或
,或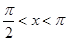
则 在
在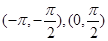 上单调递增,在
上单调递增,在  上单调递减
上单调递减
(Ⅱ)当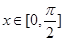 时,
时, 单调递增,
单调递增,
∴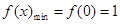 则依题
则依题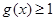 在
在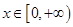 上恒成立
上恒成立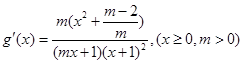
①当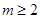 时,
时,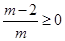 ,∴
,∴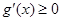 在
在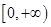 上恒成立,即
上恒成立,即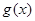 在
在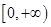 上单调递增,又
上单调递增,又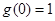 ,所以
,所以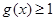 在
在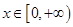 上恒成立,即
上恒成立,即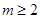 时成立
时成立
②当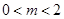 时,当
时,当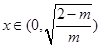 时,
时,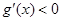 ,此时
,此时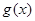 单调递减,
单调递减,
∴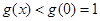 ,故
,故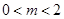 时不成立,综上
时不成立,综上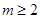
考点:本题主要考查导数的几何意义,应用导数研究函数的单调性,不等式恒成立问题。
点评:典型题,本题属于导数内容中的基本问题,(1)运用“函数在某点的切线斜率,就是该点的导数值”,确定直线的斜率。通过研究导数值的正负情况,明确函数的单调区间。不等式恒成立问题,一般的要转化成求函数的最值问题。

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
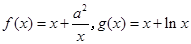 ,其中
,其中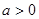 .
.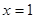 是函数
是函数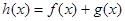 的极值点,求实数
的极值点,求实数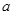 的值;
的值;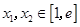 (
(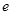 为自然对数的底数)都有
为自然对数的底数)都有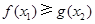 成立,求实数
成立,求实数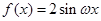 ·
·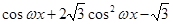 (其中
(其中 >o),且函数
>o),且函数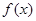 的最小正周期为
的最小正周期为
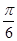 单位长度,再将所得图象各点的横坐标缩小为原来的
单位长度,再将所得图象各点的横坐标缩小为原来的 倍(纵坐标不变)得到函数y=g(x)的图象.求函数g(x)的单调区间.
倍(纵坐标不变)得到函数y=g(x)的图象.求函数g(x)的单调区间. 是△
是△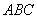 的三个内角,向量
的三个内角,向量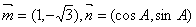 ,且
,且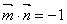
 ;
;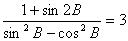 ,求
,求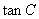 的值。
的值。
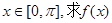 的最大值和最小值;
的最大值和最小值;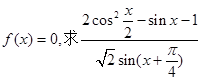 的值。
的值。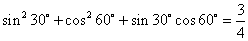 ;
;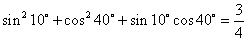 ;
;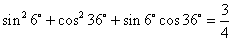 .
.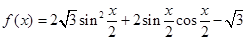 ,
,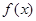 的单调递减区间;
的单调递减区间; 时,求函数
时,求函数 .
.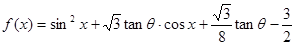 ,其中
,其中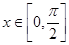 ,
,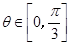
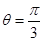 时,求
时,求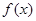 的最大值及相应的
的最大值及相应的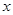 的值;
的值; ,使得函数
,使得函数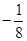 ?若存在,求出对应的
?若存在,求出对应的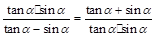 .
.