题目内容
已知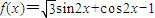
(Ⅰ)求f(x)的最小正周期和单调递增区间;
(Ⅱ)若
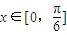 ,求f(x)的最小值及取得最小值时对应的x的取值.
,求f(x)的最小值及取得最小值时对应的x的取值.
【答案】分析:(Ⅰ)利用两角和的正弦公式,化简函数的解析式为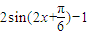 ,根据周期
,根据周期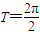 求得结果,令
求得结果,令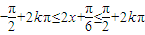 ,k∈z,求得x的范围,即可求得函数的单调递增区间.
,k∈z,求得x的范围,即可求得函数的单调递增区间.
(Ⅱ)当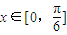 时,根据正弦函数的定义域和值域求得f(x)的最小值及取得最小值时对应的x的取值.
时,根据正弦函数的定义域和值域求得f(x)的最小值及取得最小值时对应的x的取值.
解答:解:(Ⅰ)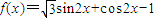 =
=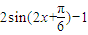 …(4分)
…(4分)
∵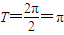 ,∴f(x)最小正周期为π.…(5分)
,∴f(x)最小正周期为π.…(5分)
由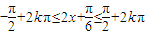 (k∈Z),得 …(6分)
(k∈Z),得 …(6分)
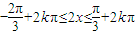 …(7分)
…(7分)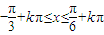 …(8分)
…(8分)
∴f(x)单调递增区间为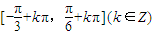 .…(9分)
.…(9分)
(Ⅱ)当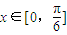 时,
时,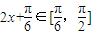 ,…(10分)
,…(10分)
∴f(x)在区间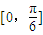 单调递增,…(11分)
单调递增,…(11分)
∴[f(x)]min=f(0)=0,对应的x的取值为0.…(13分)
点评:本题主要考查两角和的正弦公式,正弦函数的单调性、周期性、定义域和值域,属于中档题.
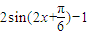 ,根据周期
,根据周期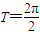 求得结果,令
求得结果,令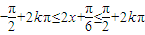 ,k∈z,求得x的范围,即可求得函数的单调递增区间.
,k∈z,求得x的范围,即可求得函数的单调递增区间.(Ⅱ)当
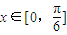 时,根据正弦函数的定义域和值域求得f(x)的最小值及取得最小值时对应的x的取值.
时,根据正弦函数的定义域和值域求得f(x)的最小值及取得最小值时对应的x的取值.解答:解:(Ⅰ)
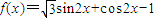 =
=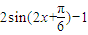 …(4分)
…(4分)∵
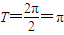 ,∴f(x)最小正周期为π.…(5分)
,∴f(x)最小正周期为π.…(5分)由
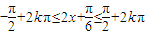 (k∈Z),得 …(6分)
(k∈Z),得 …(6分)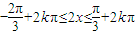 …(7分)
…(7分)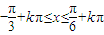 …(8分)
…(8分)∴f(x)单调递增区间为
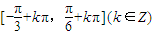 .…(9分)
.…(9分)(Ⅱ)当
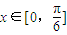 时,
时,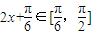 ,…(10分)
,…(10分)∴f(x)在区间
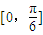 单调递增,…(11分)
单调递增,…(11分)∴[f(x)]min=f(0)=0,对应的x的取值为0.…(13分)
点评:本题主要考查两角和的正弦公式,正弦函数的单调性、周期性、定义域和值域,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
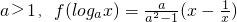
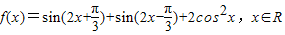
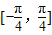 上没有零点,求m的取值范围.
上没有零点,求m的取值范围.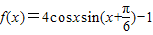
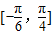 上的最大值和最小值.
上的最大值和最小值.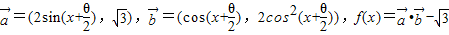

 f(α)的值.
f(α)的值.