题目内容
已知函数
(Ⅰ)求f(x)的定义域;
(Ⅱ)求f(x)的值域;
(Ⅲ)设α的锐角,且
 f(α)的值.
f(α)的值.
【答案】分析:(I)要使函数有意义需2sinx≠0,进而求得x的范围,确定函数的定义域.
(II)利用二倍角公式对函数f(x)的解析式化简整理,进而根据正弦函数的性质确定函数f(x)的值域.
(III)先利用二倍角公式,通过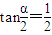 ,求得tanα,进而利用同角三角函数基本关系求得sinα和cosα,进而求得f(α)的值.
,求得tanα,进而利用同角三角函数基本关系求得sinα和cosα,进而求得f(α)的值.
解答:解:(I)由2sinx≠0,
得x≠kπ,(k∈Z),
所以f(x)的定义域为{x|x≠kπ,k∈Z}.
(II)当x≠kπ,(k∈Z)时
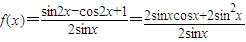 =
=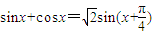 ,
,
所以f(x)的值域为 .
.
(III)因为α是锐角,且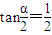 ,
,
所以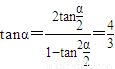 ,
,
从而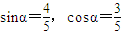 ,
,
故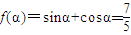 .
.
点评:本题主要考查了三角函数中恒等变换的应用,两角和公式,二倍角公式及同角三角函数基本关系的应用.考查了学生对三角函数基本公式的掌握.
(II)利用二倍角公式对函数f(x)的解析式化简整理,进而根据正弦函数的性质确定函数f(x)的值域.
(III)先利用二倍角公式,通过
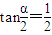 ,求得tanα,进而利用同角三角函数基本关系求得sinα和cosα,进而求得f(α)的值.
,求得tanα,进而利用同角三角函数基本关系求得sinα和cosα,进而求得f(α)的值.解答:解:(I)由2sinx≠0,
得x≠kπ,(k∈Z),
所以f(x)的定义域为{x|x≠kπ,k∈Z}.
(II)当x≠kπ,(k∈Z)时
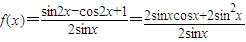 =
=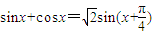 ,
,所以f(x)的值域为
 .
.(III)因为α是锐角,且
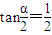 ,
,所以
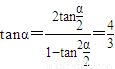 ,
,从而
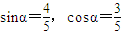 ,
,故
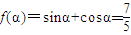 .
.点评:本题主要考查了三角函数中恒等变换的应用,两角和公式,二倍角公式及同角三角函数基本关系的应用.考查了学生对三角函数基本公式的掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
.
 .
. 上的最大值和最小值.
上的最大值和最小值. .
. ,求f(α).
,求f(α). .
. 上的最大值和最小值.
上的最大值和最小值.