题目内容
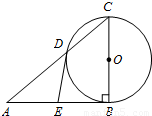
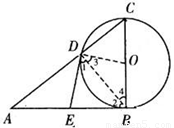
A.选修4-1:几何证明选讲如图,直角△ABC中,∠B=90°,以BC为直径的⊙O交AC于点D,点E是AB的中点.
求证:DE是⊙O的切线.
B.选修4-2:矩阵与变换
已知二阶矩阵A有特征值-1及其对应的一个特征向量为
 ,点P(2,-1)在矩阵A对应的变换下得到点P′(5,1),求矩阵A.
,点P(2,-1)在矩阵A对应的变换下得到点P′(5,1),求矩阵A.C.选修4-4:坐标系与参数方程
在直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.已知直线l的极坐标方程为
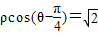 ,曲线C的参数方程为
,曲线C的参数方程为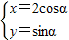 (α为参数),求曲线C截直线l所得的弦长.
(α为参数),求曲线C截直线l所得的弦长.D.选修4-5:不等式选讲
已知a,b,c都是正数,且abc=8,求证:log2(2+a)+log2(2+b)+log2(2+c)≥6.
【答案】分析:A.连接OD,DB,由BC是⊙O的直径,知∠ADB=∠CDB=90°,由此能够推导出∠EDO=∠OBE=90°,从而证明DE是⊙O的切线.
B.设二阶矩阵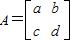 ,由题意,
,由题意,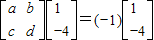 ,且
,且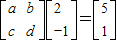 ,由此能求出矩阵A.
,由此能求出矩阵A.
C.分别把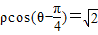 和参数方程
和参数方程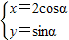 (α为参数)化为直角坐标方程,然后联立方程组解得两曲线的交点,由此能求出弦长.
(α为参数)化为直角坐标方程,然后联立方程组解得两曲线的交点,由此能求出弦长.
D.先利用基本不等式根据已知条件推导出(2+a)(2+b)(2+c)≥2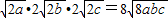 =64,再由对数性质能够证明log2(2+a)+log2(2+b)+log2(2+c)≥6.
=64,再由对数性质能够证明log2(2+a)+log2(2+b)+log2(2+c)≥6.
解答:【选做题】在A、B、C、D四小题中只能选做两题,每小题(10分),共计(20分).
A.选修4-1:几何证明选讲
证:连接OD,DB
∵BC是⊙O的直径∴∠ADB=∠CDB=90°…(2分)
∵E是AB的中点∴DE= AB=EB∴∠1=∠2
AB=EB∴∠1=∠2
∵OD=OB,∴∠3=∠4…(8分)
∴∠1+∠3=∠2+∠4.即∠EDO=∠OBE=90°
∴DE是⊙O的切线.…(10分)
B.选修4-2:矩阵与变换
解:设二阶矩阵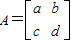
由题意,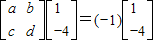 ,且
,且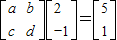 …(4分)
…(4分)
即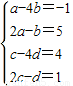 ,…(8分)
,…(8分)
解得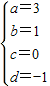 ,∴
,∴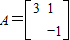 .…(10分)
.…(10分)
C.选修4-4:坐标系与参数方程
解:由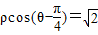 ,化为直角坐标方程x+y-2=0,①…(4分)
,化为直角坐标方程x+y-2=0,①…(4分)
参数方程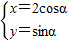 (α为参数),化为直角坐标方程
(α为参数),化为直角坐标方程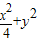 =1,②…(8分)
=1,②…(8分)
联立①②得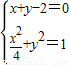 ,解得两曲线的交点为(2,0),
,解得两曲线的交点为(2,0),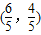 ,
,
所以所求的弦长=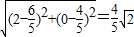 .…(10分)
.…(10分)
D.选修4-5:不等式选讲
证明:∵a,b,c都是正数,
∴2+a≥2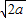 ,2+b≥2
,2+b≥2 ,2+c≥2
,2+c≥2 ,…(4分)
,…(4分)
又∵abc=8,
∴(2+a)(2+b)(2+c)≥2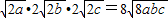 =64,…(8分)
=64,…(8分)
(当且仅当a=b=c=2时等号成立)…(9分)
故log2(2+a)+log2(2+b)+log2(2+c)
=log2[(2+a)(2+b)(2+c)]
≥log264=6.…(10分)
点评:A考查与圆有关的比例线段,B考查矩阵与变换,C考查极坐标与参数方程,D考查不等式的证明,都是中档题.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.
B.设二阶矩阵
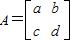 ,由题意,
,由题意,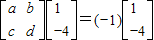 ,且
,且 ,由此能求出矩阵A.
,由此能求出矩阵A.C.分别把
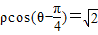 和参数方程
和参数方程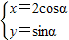 (α为参数)化为直角坐标方程,然后联立方程组解得两曲线的交点,由此能求出弦长.
(α为参数)化为直角坐标方程,然后联立方程组解得两曲线的交点,由此能求出弦长.D.先利用基本不等式根据已知条件推导出(2+a)(2+b)(2+c)≥2
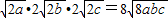 =64,再由对数性质能够证明log2(2+a)+log2(2+b)+log2(2+c)≥6.
=64,再由对数性质能够证明log2(2+a)+log2(2+b)+log2(2+c)≥6.解答:【选做题】在A、B、C、D四小题中只能选做两题,每小题(10分),共计(20分).
A.选修4-1:几何证明选讲
证:连接OD,DB
∵BC是⊙O的直径∴∠ADB=∠CDB=90°…(2分)
∵E是AB的中点∴DE=
 AB=EB∴∠1=∠2
AB=EB∴∠1=∠2∵OD=OB,∴∠3=∠4…(8分)
∴∠1+∠3=∠2+∠4.即∠EDO=∠OBE=90°
∴DE是⊙O的切线.…(10分)

B.选修4-2:矩阵与变换
解:设二阶矩阵
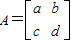
由题意,
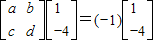 ,且
,且 …(4分)
…(4分)即
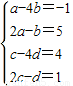 ,…(8分)
,…(8分)解得
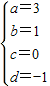 ,∴
,∴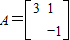 .…(10分)
.…(10分)C.选修4-4:坐标系与参数方程
解:由
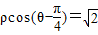 ,化为直角坐标方程x+y-2=0,①…(4分)
,化为直角坐标方程x+y-2=0,①…(4分)参数方程
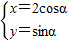 (α为参数),化为直角坐标方程
(α为参数),化为直角坐标方程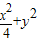 =1,②…(8分)
=1,②…(8分)联立①②得
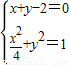 ,解得两曲线的交点为(2,0),
,解得两曲线的交点为(2,0),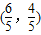 ,
,所以所求的弦长=
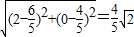 .…(10分)
.…(10分)D.选修4-5:不等式选讲
证明:∵a,b,c都是正数,
∴2+a≥2
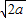 ,2+b≥2
,2+b≥2 ,2+c≥2
,2+c≥2 ,…(4分)
,…(4分)又∵abc=8,
∴(2+a)(2+b)(2+c)≥2
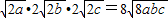 =64,…(8分)
=64,…(8分)(当且仅当a=b=c=2时等号成立)…(9分)
故log2(2+a)+log2(2+b)+log2(2+c)
=log2[(2+a)(2+b)(2+c)]
≥log264=6.…(10分)
点评:A考查与圆有关的比例线段,B考查矩阵与变换,C考查极坐标与参数方程,D考查不等式的证明,都是中档题.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
相关题目
 A(选修4-1:几何证明选讲)
A(选修4-1:几何证明选讲) 选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.
选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤. A)选修4-1:几何证明选讲
A)选修4-1:几何证明选讲 选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分. 从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)
从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)