题目内容
 A(选修4-1:几何证明选讲)
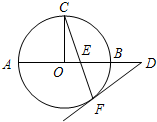
A(选修4-1:几何证明选讲)如图,AB是⊙O的直径,C,F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D,连接CF交AB于点E.
求证:DE2=DB•DA.
B(选修4-2:矩阵与变换)
求矩阵
|
C(选修4-4:坐标系与参数方程)
已知曲线C的极坐标方程是ρ=2sinθ,直线l的参数方程是
|
(Ⅰ)将曲线C的极坐标方程化为直角坐标方程;
(Ⅱ)设直线l与x轴的交点是M,N是曲线C上一动点,求MN的最大值.
D(选修4-5:不等式选讲)
已知m>0,a,b∈R,求证:(
| a+mb |
| 1+m |
| a2+mb2 |
| 1+m |
分析:A、由已知中AB是⊙O的直径,C,F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D,连接CF交AB于点E.由线割线定理我们易得DF2=DB•DA,故我们仅需要证明DE=DF即可得到结论.
B、构造特征多项式,求出特征值λ的值,再将特征值λ的值代入特征方程组,即可求出特征向量.
C、根据曲线C的极坐标方程是ρ=2sinθ,直线l的参数方程是
(t为参数).我们易求出曲线C的标准方程及直线l的一般方程,利用直线一圆的位置关系,判断圆心到直线的距离与半径的关系,即可得到答案.
D、因为m>0,所以1+m>0,结合不等式性质,可将原不等式化为一个整式不等式,然后利用完成平方公式配方后,即可得到结论.
B、构造特征多项式,求出特征值λ的值,再将特征值λ的值代入特征方程组,即可求出特征向量.
C、根据曲线C的极坐标方程是ρ=2sinθ,直线l的参数方程是
|
D、因为m>0,所以1+m>0,结合不等式性质,可将原不等式化为一个整式不等式,然后利用完成平方公式配方后,即可得到结论.
解答:证明:A,连接OF,因为DF切⊙O于F,所以∠OFD=90°,所以∠OFC+∠CFD=90°.
因为OC=OF,所以∠OCF=∠OFC,又因为CO⊥AB于O,
所以∠OCF+∠CEO=90°(5分)
所以∠CFD=∠CEO=∠DEF,所以DF=DE,因为DF是⊙O的切线,所以DF2=DB•DA.
所以DE2=DB•DA(10分)
B,特征多项式f(λ)=
=(λ-2)2-1=λ2-4λ+3(3分)
由f(λ)=0,解得λ1=1,λ2=3(6分)将λ1=1代入特征方程组,得
?x+y=0,可取
为属于特征值λ1=1的一个特征向量(8分)
同理,当λ2=3时,由
?x-y=0,所以可取
为属于特征值λ2=3的一个特征向量.
综上所述,矩阵
有两个特征值λ1=1,λ2=3;属于λ1=1的一个特征向量为
,
属于λ2=3的一个特征向量为
(10分)
C(Ⅰ)曲线C的极坐标方程可化为ρ2=2ρsinθ(2分)
又x2+y2=ρ2,x=ρcosθ,y=ρsinθ,所以曲线C的直角坐标方程为x2+y2-2y=0(4分)
(Ⅱ)将直线l的参数方程化为直角坐标方程,得y=-
(x-2)(6分)
令y=0,得x=2,即M点的坐标为(2,0).又曲线C为圆,圆C的圆心坐标为(1,0),
半径r=1,则|MC|=
(8分)
所以|MN|≤|MC|+r=
+1(10分)
D.因为m>0,所以1+m>0,所以要证(
)2≤
,即证(a+mb)2≤(1+m)(a2+mb2),
即证m(a2-2ab+b2)≥0,即证(a-b)2≥0,
而(a-b)2≥0显然成立,故(
)2≤
(10分)
因为OC=OF,所以∠OCF=∠OFC,又因为CO⊥AB于O,
所以∠OCF+∠CEO=90°(5分)
所以∠CFD=∠CEO=∠DEF,所以DF=DE,因为DF是⊙O的切线,所以DF2=DB•DA.
所以DE2=DB•DA(10分)
B,特征多项式f(λ)=
|
由f(λ)=0,解得λ1=1,λ2=3(6分)将λ1=1代入特征方程组,得
|
|
同理,当λ2=3时,由
|
|
综上所述,矩阵
|
|
属于λ2=3的一个特征向量为
|
C(Ⅰ)曲线C的极坐标方程可化为ρ2=2ρsinθ(2分)
又x2+y2=ρ2,x=ρcosθ,y=ρsinθ,所以曲线C的直角坐标方程为x2+y2-2y=0(4分)
(Ⅱ)将直线l的参数方程化为直角坐标方程,得y=-
| 4 |
| 3 |
令y=0,得x=2,即M点的坐标为(2,0).又曲线C为圆,圆C的圆心坐标为(1,0),
半径r=1,则|MC|=
| 5 |
所以|MN|≤|MC|+r=
| 5 |
D.因为m>0,所以1+m>0,所以要证(
| a+mb |
| 1+m |
| a2+mb2 |
| 1+m |
即证m(a2-2ab+b2)≥0,即证(a-b)2≥0,
而(a-b)2≥0显然成立,故(
| a+mb |
| 1+m |
| a2+mb2 |
| 1+m |
点评:本题考查的知识点是与圆相关的比例线段,特征值与特征向量的计算,参数方程化为普通方程,不等式的证明,是高考的四选一考题,我们只需要根据自己的情况选择其一作答即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.
选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤. A)选修4-1:几何证明选讲
A)选修4-1:几何证明选讲 选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分. 从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)
从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)