题目内容
【题目】如图所示，在三棱锥A﹣BCD中，E，F，G，H分别是棱AB，BC，CD，DA的中点，则当AC，BD满足条件 时，四边形EFGH为菱形．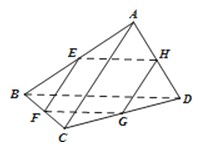
【答案】AC=BD
【解析】解：在三棱锥A﹣BCD中，
∵E，F，G，H分别是棱AB，BC，CD，DA的中点，
∴EH
BD，FGBD，∴EHFG，
EFAC，HGAC，∴EFHG，
∴四边形EFGH为平行四边形，
∵四边形EFGH为菱形，∴EF=EH，∴AC=BD，
∴当AC，BD满足条件AC=BD时，四边形EFGH为菱形．
所以答案是：AC=BD．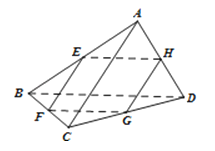
【考点精析】本题主要考查了直线与平面平行的性质的相关知识点，需要掌握一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行;简记为：线面平行则线线平行才能正确解答此题．
练习册系列答案
名题金卷系列答案
相关题目
【题目】一台机器由于使用时间较长，生产的零件有一些缺损．按不同转速生产出来的零件有缺损的统计数据如下表所示：
转速x(转/秒) | 16 | 4 | 12 | 8 |
每小时生产有缺损零件数y(个) | 11 | 9 | 8 | 5 |
(1)作出散点图；
(2)如果y与x线性相关，求出回归直线方程；
(3)若实际生产中，允许每小时的产品中有缺损的零件最多为10个，那么，机器的运转速度应控制在什么范围内？
