题目内容
已知sinα，cosα是关于x的一元二次方程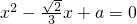
的两根，其中α∈[0，π]
（1）求α的值．
（2）求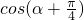
的值．
解：（1）由韦达定理，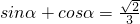
①，sinα•cosα=a②
①式平方，得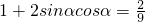
∴
③
∴
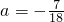
（2）∵
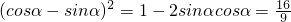
又α∈[0，π]，sinα＞0由③知cosα＜0
∴
∴
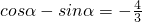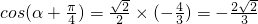
分析：（1）由韦达定理，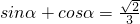
①，sinα•cosα=a②，利用同角平方关系联立①②可求a的值
（2∵（sinα-cosα）2=1-2sinαcosα=
，结合（1）可知α∈[0，π]，sinα＞0，cosα＜0，从而可得sinα-cosα，又
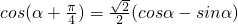，代入可求
点评：本题主要考查了利用同角平方关系建立sinα+cosα，与sinα-cosα，与sinαcosα之间的关系，考查了两角和的余弦公式．
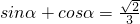①，sinα•cosα=a②①式平方，得
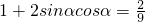∴③∴
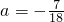
（2）∵
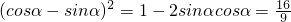
又α∈[0，π]，sinα＞0由③知cosα＜0
∴
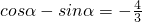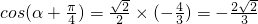
∴分析：（1）由韦达定理，
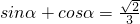①，sinα•cosα=a②，利用同角平方关系联立①②可求a的值（2∵（sinα-cosα）2=1-2sinαcosα=
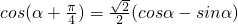，结合（1）可知α∈[0，π]，sinα＞0，cosα＜0，从而可得sinα-cosα，又，代入可求点评：本题主要考查了利用同角平方关系建立sinα+cosα，与sinα-cosα，与sinαcosα之间的关系，考查了两角和的余弦公式．
练习册系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目