题目内容
9.已知奇函数f(x)在定义域(-2,2)内是单调递增函数,求满足f(1-m)+f(1-3m)<0的实数m的取值范围.分析 根据函数奇偶性和单调性的关系进行转化再求解即可.
解答 解:∵奇函数f(x)在定义域(-2,2)内是单调递增函数,
∴由f(1-m)+f(1-3m)<0得f(1-m)<-f(1-3m)=f(3m-1),
∴-2<1-m<3m-1<2,
解得$\frac{1}{2}$<m<1,
即实数m的取值范围是($\frac{1}{2}$,1).
点评 本题主要考查不等式的求解,根据函数奇偶性和单调性之间的关系是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19. 如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,
如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,
①AD⊥MN; ②MN∥面CDE;
③MN∥CE; ④MN、CE异面.
其中正确结论的个数是( )
 如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,
如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,①AD⊥MN; ②MN∥面CDE;
③MN∥CE; ④MN、CE异面.
其中正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.设f(x)是定义在R上的函数,则“函数f(x)为偶函数”是“函数xf(x)为奇函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
14.已知a>b>0,椭圆C1的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,双曲线C2的方程为$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$,C1与C2的离心率之积为$\frac{{\sqrt{3}}}{2}$,则双曲线C2的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
18.椭圆$\frac{x^2}{4}+\frac{y^2}{2+k}=1$的离心率为$\frac{1}{2}$,则k的值为( )
| A. | $-\frac{10}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{10}{3}$或1 | D. | $-\frac{10}{3}$或1 |
 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作与截面PBC1平行的截面,则截面的面积是2$\sqrt{6}$.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作与截面PBC1平行的截面,则截面的面积是2$\sqrt{6}$.
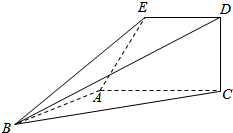 如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=90°,∠EAC=60°,AB=AC.
如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=90°,∠EAC=60°,AB=AC.