题目内容
3.设函数f(x)=$\left\{\begin{array}{l}{2{x}^{2}-1,(x≤0)}\\{lo{g}_{2}x,(x>0)}\end{array}\right.$,则不等式f(x)<1的解集是( )| A. | (-1,2) | B. | (-∞,2) | C. | (1,+∞) | D. | (-∞,-1)∩(2,+∞) |
分析 由分段函数对x分类,把f(x)<1化为二次不等式和对数不等式求解,最后取并集得答案.
解答 解:当x≤0时,f(x)<1化为$\left\{\begin{array}{l}{x≤0}\\{2{x}^{2}-1<1}\end{array}\right.$,解得:-1<x≤0;
当x>0时,f(x)<1化为$\left\{\begin{array}{l}{x>0}\\{lo{g}_{2}x<1}\end{array}\right.$,解得:0<x<2.
∴不等式f(x)<1的解集是(-1,2).
故选:A.
点评 本题考查了指数不等式和对数不等式的解法,考查了分类讨论的数学思想方法,属中档题.

练习册系列答案
相关题目
18.某几何体的三视图如图所示,则此几何体不可能是( )


| A. | 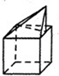 | B. |  | C. |  | D. |  |
8.函数y=sin(π-x)-1的图象( )
| A. | 关于x=$\frac{π}{2}$对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于x=π对称 |
15.已知集合A={x|y=$\sqrt{{x}^{2}-2x-3}$},B={y|y=3sinx-1},则集合B∩∁RA=( )
| A. | (-1,2] | B. | ∅ | C. | [-4,-1] | D. | [-4,3) |
12.在极坐标系中,曲线ρ=2cosθ是( )
| A. | 过极点的直线 | B. | 半径为2 的圆 | ||
| C. | 关于极点对称的图形 | D. | 关于极轴对称的图形 |