题目内容
13.已知O是△ABC的外接圆圆心,$|\overrightarrow{AB}|=4$,$|\overrightarrow{AC}|=2$,∠ABC=30°,若D是BC中点,则$\overrightarrow{AO}•\overrightarrow{AD}$=5.分析 根据条件得出$\overrightarrow{AD}$=$\overrightarrow{AC}$+$\frac{1}{2}$$\overrightarrow{CB}$,$\overrightarrow{AO}$=$\frac{1}{2}$$\overrightarrow{AB}$=$\frac{1}{2}\overrightarrow{AC}$$+\frac{1}{2}\overrightarrow{CB}$,利用正弦定理得出∠ACB=90°,∠ACB=60°,CB=2$\sqrt{3}$,展开$\overrightarrow{AO}•\overrightarrow{AD}$=($\overrightarrow{AC}$$+\frac{1}{2}\overrightarrow{CB}$)•($\frac{1}{2}\overrightarrow{AC}$$+\frac{1}{2}\overrightarrow{CB}$)代入即可.
解答 解:∵O是△ABC的外接圆圆心,$|\overrightarrow{AB}|=4$,$|\overrightarrow{AC}|=2$,∠ABC=30°,若D是BC中点,
∴$\overrightarrow{AD}$=$\overrightarrow{AC}$+$\frac{1}{2}$$\overrightarrow{CB}$,$\overrightarrow{AO}$=$\frac{1}{2}$$\overrightarrow{AB}$=$\frac{1}{2}\overrightarrow{AC}$$+\frac{1}{2}\overrightarrow{CB}$,
$\frac{|\overrightarrow{AC}|}{sin30°}$=$\frac{|\overrightarrow{AB}|}{sin∠ACB}$,
即sin∠ACB=1,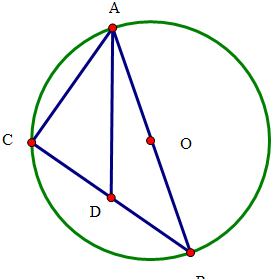
∴$\overrightarrow{AO}•\overrightarrow{AD}$=($\overrightarrow{AC}$$+\frac{1}{2}\overrightarrow{CB}$)•($\frac{1}{2}\overrightarrow{AC}$$+\frac{1}{2}\overrightarrow{CB}$)=
$\frac{1}{2}×{2}^{2}$$+\frac{3}{4}$$\overrightarrow{AC}$$•\overrightarrow{CB}$$+\frac{1}{4}$×(2$\sqrt{3}$)2=2+0+3=5
故答案为:5
点评 本题考查了三角形中的边角关系,平面向量的运算,数量积的计算,难度不大,仔细写即可,属于中档题.

 智能训练练测考系列答案
智能训练练测考系列答案| A. | (-1,2) | B. | (-∞,2) | C. | (1,+∞) | D. | (-∞,-1)∩(2,+∞) |
| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | $\frac{{\sqrt{5}+2}}{2}$ | C. | $\frac{{\sqrt{3}+1}}{2}$ | D. | $\frac{3}{2}$ |
 已知某个几何体的三视图如图,根据图中标出的尺寸,可得这个几何体的体积等于$\frac{8}{3}$,全面积为2(3+$\sqrt{2}$+$\sqrt{5}$).
已知某个几何体的三视图如图,根据图中标出的尺寸,可得这个几何体的体积等于$\frac{8}{3}$,全面积为2(3+$\sqrt{2}$+$\sqrt{5}$).