题目内容
.若果数列 的项构成的新数列
的项构成的新数列 是公比为
是公比为 的等比数
的等比数 列,则相应的数列
列,则相应的数列 是公比为
是公比为 的等比数列,运用此性质,可以较为简洁的求出一类递推数列的通项公式,并简称此法为双等比数列法.已知数列
的等比数列,运用此性质,可以较为简洁的求出一类递推数列的通项公式,并简称此法为双等比数列法.已知数列 中,
中, ,
, ,且
,且 .
.
(1)试利用双等比数列法求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和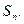
 的项构成的新数列
的项构成的新数列 是公比为
是公比为 的等比数
的等比数 列,则相应的数列
列,则相应的数列 是公比为
是公比为 的等比数列,运用此性质,可以较为简洁的求出一类递推数列的通项公式,并简称此法为双等比数列法.已知数列
的等比数列,运用此性质,可以较为简洁的求出一类递推数列的通项公式,并简称此法为双等比数列法.已知数列 中,
中, ,
, ,且
,且 .
.(1)试利用双等比数列法求数列
 的通项公式;
的通项公式;(2)求数列
 的前
的前 项和
项和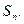
解:(1)有条件知: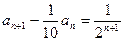 ,①所以
,①所以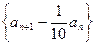 是公比为
是公比为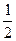 的等比数列,
的等比数列,
故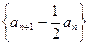 是以首项为
是以首项为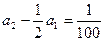 ,公比为
,公比为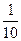 的等比数列,
的等比数列,
所以: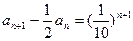 ,②
,②
由①、②得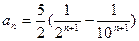 。
。
(2)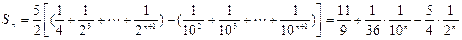
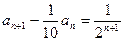 ,①所以
,①所以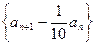 是公比为
是公比为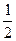 的等比数列,
的等比数列,故
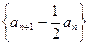 是以首项为
是以首项为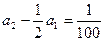 ,公比为
,公比为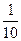 的等比数列,
的等比数列,所以:
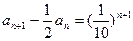 ,②
,②由①、②得
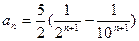 。
。(2)
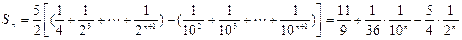
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的前
的前 项和
项和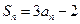
 .
.
 ,且
,且 ,求数列
,求数列 的前
的前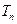
 ,数列{ Sn +2}是以2为公比的等比数列.
,数列{ Sn +2}是以2为公比的等比数列. ;
;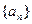 满足:
满足: ,其中
,其中 为数列
为数列 项和.(Ⅰ)试求
项和.(Ⅰ)试求 Ⅱ)若数列
Ⅱ)若数列 满足:
满足: ,试求
,试求 项和公式
项和公式 ;(III)设
;(III)设 ,数列
,数列 的前
的前 ,求证:
,求证: .
. 中,
中, ,求
,求
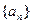 满足
满足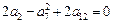 ,且数列
,且数列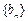 是等比数列,若
是等比数列,若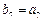 ,则
,则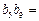
 中,已知
中,已知 ,则公比为
,则公比为 2
2 



 2或4
2或4 }的前n项和为
}的前n项和为 ,若
,若 ()
()