题目内容
已知椭圆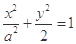
的一个焦点与抛物线
的焦点重合,则该椭圆的离心率是( ）
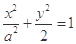的一个焦点与抛物线的焦点重合,则该椭圆的离心率是( ）A． | B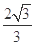． | C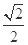． | D． |
D
抛物线的焦点坐标为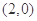
，所以椭圆中的
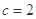。所以
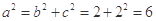，即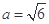
。所以椭圆的离心率为
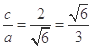，选D
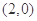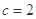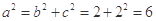，所以椭圆中的。所以，即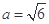。所以椭圆的离心率为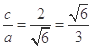，选D
练习册系列答案
相关题目
题目内容
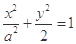的一个焦点与抛物线的焦点重合,则该椭圆的离心率是( ）| A． | B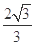． | C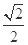． | D． |
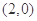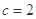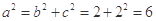，所以椭圆中的。所以，即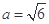。所以椭圆的离心率为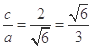，选D
的长轴长为
，离心率为
，
分别为其左右焦点．一动圆过点
，且与直线
相切．
的方程；（ⅱ)求动圆圆心轨迹
的方程；
，满足
与
共线，
与
共线，且
，求四边形
面积的最小值．
的离心率
，长轴的左右端点分别为
，
．
与曲线
，且与直线
相交于点
.问在
轴上是否存在定点
，使得以
为直径的圆恒过定点
，
、
是椭圆的左右焦点，且椭圆经过点
.
且倾斜角等于
的直线
，交椭圆于
、
两点，求
的面积.
=1（a＞b＞0）的左、右焦点分别为为
，
恰是抛物线C2：
的焦点，点M为C1与C2在第一象限的交点，且｜MF2｜=
．
，直线l∥MN，且与C1交于A，B两点，若
，求直线l的方程．
，点
，P是圆E上任意一点．线段PF的垂直平分线和半径PE相交于Q．
的方程；
，
，点G是轨迹
相交于点D，试判断以线段BD为直径的圆与直线GF的位置关系，并证明你的结论．
所截得的线段的中点，则l的方程是( )
的离心率
，右焦点
，方程
的两个根分别为
,则点
在（ ）
上
的右焦点为
，椭圆
与
轴正半轴交于
点，与
轴正半轴交于
，且
，则椭圆
