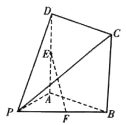
题目内容
【题目】如图，已知点E是正方形ABCD边AD的中点，现将△ABE沿BE所在直线翻折成到△A'BE，使A’C=BC，并连接A'C，A'D．
（1）求证：DE∥平面A'BC；
（2）求证：A'E⊥平面A'BC．
【答案】（1）见解析；（2）见解析
【解析】
（1）推导出DE∥BC，由此能证明DE∥平面A′BC；（2）设正方形ABCD的边长为a，连接EC．推导出A′E⊥A′C，A′E⊥A′B，由此能证明A'E⊥平面A'BC．
（1）∵正方形ABCD中，DE∥BC，
又DE平面A′BC，BC平面A′BC，
∴DE∥平面A′BC．
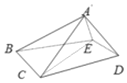
（2）不妨设正方形ABCD的边长为a，连接EC．
在△A′CE中，
，EC=
，A′C=a，
满足A′E2+A′C2=EC2，∴A′E⊥A′C，
又A′E⊥A′B，且A′B∩A′C=A′，A′B平面A′BC，
A′C平面A′BC，∴A'E⊥平面A'BC．
【题目】近年空气质量逐步雾霾天气现象增多，大气污染危害加重，大气污染可引起心悸，呼吸困难等心肺疾病，为了解某市心肺疾病是否与性别有关，在某医院随机的对入院50人进行了问卷调查得到了如下的列联表：
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 5 | ||
女 | 10 | ||
合计 | 50 |
已知按性别采用分层抽样法抽取容量为10的样本，则抽到男士的人数为5．
（Ⅰ）请将上面的列联表补充完整；
（Ⅱ）能否在犯错概率不超过
的前提下认为患心肺疾病与性别有关？说明你的理由．
下面的临界值表供参考：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式：
，其中
【题目】企业需为员工缴纳社会保险，缴费标准是根据职工本人上一年度月平均工资（单位：元）的
缴纳，
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
t | 1 | 2 | 3 | 4 | 5 |
y | 270 | 330 | 390 | 460 | 550 |
某企业员工甲在2014年至2018年各年中每月所撒纳的养老保险数额y（单位：元）与年份序号t的统计如下表：
（1）求出t关于t的线性回归方程
；
（2）试预测2019年该员工的月平均工资为多少元？
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
（注：
，
，其中
）
【题目】襄阳市拟在2021年奥体中心落成后申办2026年湖北省省运会，据了解，目前武汉，宜昌，黄石等申办城市因市民担心赛事费用超支而准备相继退出，某机构为调查襄阳市市民对申办省运会的态度，选取某小区的100位居民调查结果统计如下：
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 60 | ||
年龄大于50岁 | 10 | ||
合计 | 80 | 100 |
（1）根据已知数据，把表格数据填写完整；
（2）能否在犯错误的概率不超过
的前提下认为不同年龄与支持申办省运会无关？
附： 
, 
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
