题目内容
袋中共有10个大小相同的编号为1,2,3的球，其中1号球有1个，2号球有m个，3号球有n个．从袋中依次摸出2个球，已知在第一次摸出3号球的前提下，再摸出一个2号球的概率是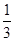
．
(1)求m，n的值；
(2)从袋中任意摸出2个球，设得到小球的编号数之和为ξ，求随机变量ξ的分布列．
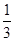．(1)求m，n的值；
(2)从袋中任意摸出2个球，设得到小球的编号数之和为ξ，求随机变量ξ的分布列．
（1）m＝3，n＝6
（2）
（2）
| ξ | 3 | 4 | 5 | 6 |
| P |  |  |  | |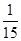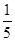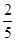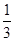
(1)记“第一次摸出3号球”为事件A，“第二次摸出2号球”为事件B，则P(B|A)＝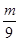
＝，
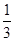∴m＝3，n＝10－3－1＝6．
(2)由(1)知10个球中有1号球1个，2号球3个，3号球6个，则ξ的可能取值为3,4,5,6．
P(ξ＝3)＝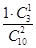
＝，
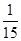P(ξ＝4)＝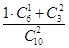
＝，
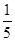P(ξ＝5)＝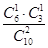
＝，
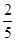P(ξ＝6)＝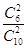
＝．
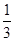故ξ的分布列为
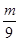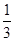＝，∴m＝3，n＝10－3－1＝6．
(2)由(1)知10个球中有1号球1个，2号球3个，3号球6个，则ξ的可能取值为3,4,5,6．
P(ξ＝3)＝
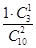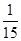＝，P(ξ＝4)＝
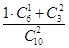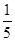＝，P(ξ＝5)＝
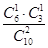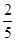＝，P(ξ＝6)＝
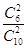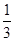＝．故ξ的分布列为
| ξ | 3 | 4 | 5 | 6 |
| P | | | | |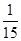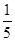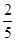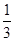
练习册系列答案
相关题目
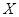表示在这块地上种植1季此作物的利润，求
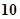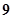环、
环、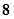
环的概率分别是
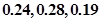，则这位射手在一次射击中不够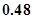
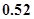
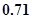
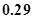
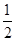
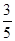
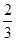
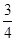
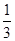
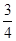
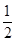成等差数列，
．；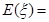