题目内容
在一块耕地上种植一种作物,每季种植成本为1000元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:

(1)设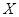 表示在这块地上种植1季此作物的利润,求
表示在这块地上种植1季此作物的利润,求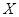 的分布列;
的分布列;
(2)若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于2000元的概率.

(1)设
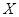 表示在这块地上种植1季此作物的利润,求
表示在这块地上种植1季此作物的利润,求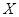 的分布列;
的分布列;(2)若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于2000元的概率.
(1)分布列见解析;(2)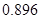 .
.
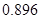 .
.试题分析:(1)设
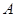 表示事件“作物产量为300
表示事件“作物产量为300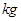 ”,
”,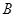 表示事件“作物市场价格为6元
表示事件“作物市场价格为6元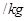 ”
”由题设得4000,2000,800,结合概率公式计算出对应的概率,得出分布列;
(2)设
 表示事件“第
表示事件“第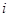 季利润不少于2000元”
季利润不少于2000元”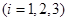 ,由题意知:
,由题意知: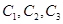 相互独立,由(1)知
相互独立,由(1)知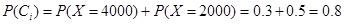
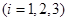 ,3季利润均不少于2000元的概率为:
,3季利润均不少于2000元的概率为: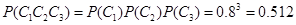 ,3季中有2季利润不少于2000元的概率为:
,3季中有2季利润不少于2000元的概率为: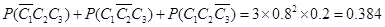 ,根据互斥事件概率的加法公式得:这3季中至少有2季的利润不少于2000元的概率为:
,根据互斥事件概率的加法公式得:这3季中至少有2季的利润不少于2000元的概率为: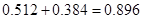
试题解析:(1)设
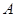 表示事件“作物产量为300
表示事件“作物产量为300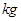 ”,
”,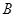 表示事件“作物市场价格为6元
表示事件“作物市场价格为6元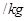 ”
”由题设知:
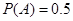 ,
,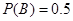
因为利润=产量
 市场价格-成本
市场价格-成本所以
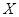 所以可能的取值为
所以可能的取值为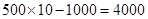 ,
,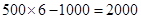
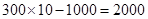 ,
,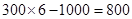
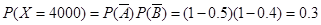 ,
,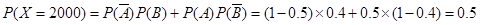 ,
,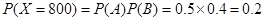 ,
,所以
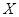 的分布列为
的分布列为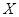 | 4000 | 2000 | 800 |
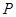 | 0.3 | 0.5 | 0.2 |
 表示事件“第
表示事件“第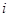 季利润不少于2000元”
季利润不少于2000元”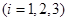 ,
,由题意知:
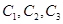 相互独立,由(1)知
相互独立,由(1)知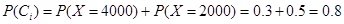
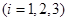
3季利润均不少于2000元的概率为:
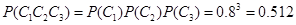
3季中有2季利润不少于2000元的概率为:
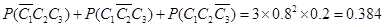
所以,这3季中至少有2季的利润不少于2000元的概率为:
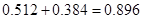

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
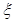 .
.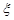 的数学期望和方差.
的数学期望和方差.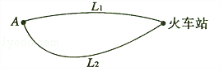
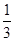 .
.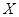 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量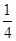 ,不堵车的概率为
,不堵车的概率为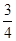 ;校车走公路②堵车的概率为
;校车走公路②堵车的概率为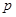 ,不堵车的概率为
,不堵车的概率为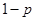 .若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响. ,求走公路②堵车的概率;
,求走公路②堵车的概率;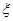 的分布列和数学期望.
的分布列和数学期望.