题目内容
12.在△ABC中,∠A=$\frac{π}{3}$,$\overrightarrow{m}$=(cosB,-sinB),$\overrightarrow{n}$=(cosC,sinC).(1)求$\overrightarrow{m}$•$\overrightarrow{n}$的大小;
(2)若a、b、c为角A、B、C的对边,a=2,cosB=$\frac{\sqrt{3}}{3}$,求b的长.
分析 (1)利用向量的数量积公式,结合和角的余弦公式,即可求$\overrightarrow{m}$•$\overrightarrow{n}$的大小;
(2)求出sinB=$\frac{\sqrt{6}}{3}$,利用正弦定理,即可求b的长.
解答 解:(1)∵$\overrightarrow{m}$=(cosB,-sinB),$\overrightarrow{n}$=(cosC,sinC),
∴$\overrightarrow{m}$•$\overrightarrow{n}$=cosBcosC-sinBsinC=cos(B+C)=-cosA=-$\frac{1}{2}$;
(2)∵cosB=$\frac{\sqrt{3}}{3}$,
∴sinB=$\frac{\sqrt{6}}{3}$,
∵a=2,A=$\frac{π}{3}$,
∴由正弦定理可得b=$\frac{2×\frac{\sqrt{6}}{3}}{\frac{\sqrt{3}}{2}}$=$\frac{4}{3}$$\sqrt{2}$.
点评 本题考查向量的数量积公式,和角的余弦公式,考查正弦定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
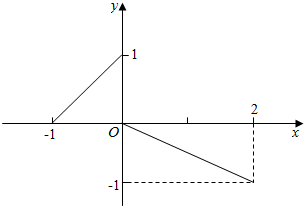
1.f(x)图象如图,则f(x)=$\left\{\begin{array}{l}{x+1}&{-1≤x≤0}\\{-\frac{1}{2}x}&{0<x≤2}\end{array}\right.$.

1.已知单位向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为120°,且|$\overrightarrow{c}$-$\overrightarrow{a}$|+|$\overrightarrow{c}$-$\overrightarrow{b}$|=$\sqrt{3}$,则|$\overrightarrow{c}$+2$\overrightarrow{a}$|的取值范围是( )
| A. | [$\frac{3}{2}$,+∞) | B. | [$\sqrt{3}$,3] | C. | [$\sqrt{3}$,+∞) | D. | [$\frac{3}{2}$,3] |