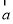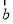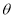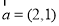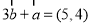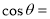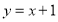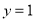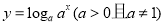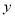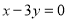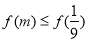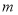题目内容
注:此题选A题考生做①②小题,选B题考生做①③小题.
已知函数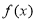 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当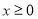 时有
时有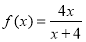 .
.
①求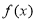 的解析式;②(选A题考生做)求
的解析式;②(选A题考生做)求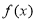 的值域;
的值域;
③(选B题考生做)若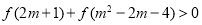 ,求
,求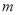 的取值范围.
的取值范围.
① ;②
;②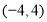 ;③
;③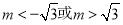
【解析】
试题分析:①当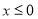 时,
时,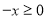 ,根据
,根据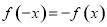 可推导出
可推导出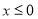 时
时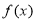 的解析式。注意最后将此函数写成分段函数的形式。②本题属用分离常数项法求函数值域。当
的解析式。注意最后将此函数写成分段函数的形式。②本题属用分离常数项法求函数值域。当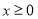 时将
时将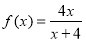 按分离常数项法将此函数化为
按分离常数项法将此函数化为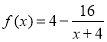 ,根据自变量的范围可推导出函数值的范围,因为此函数为奇函数所以值域也对称。故可得出
,根据自变量的范围可推导出函数值的范围,因为此函数为奇函数所以值域也对称。故可得出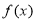 的值域。③本题属用单调性“知二求一”解不等式问题。所以应先判断此函数的单调性。同②当
的值域。③本题属用单调性“知二求一”解不等式问题。所以应先判断此函数的单调性。同②当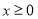 时将
时将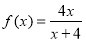 化为
化为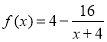 ,可知
,可知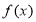 在
在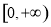 上是增函数,因为
上是增函数,因为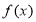 为奇函数,所以
为奇函数,所以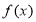 在上
在上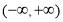 是增函数。根据单调性得两自变量的不等式,即可求得
是增函数。根据单调性得两自变量的不等式,即可求得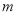 的取值范围。
的取值范围。
试题解析:【解析】
①∵当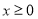 时有
时有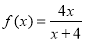 ∴当
∴当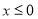 时,
时,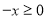 ∴
∴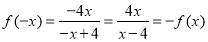 ∴
∴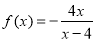 (
(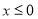 )∴
)∴ (6分)
(6分)
②∵当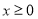 时有
时有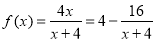 ∴
∴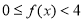 又∵
又∵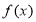 是奇函数∴当
是奇函数∴当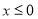 时
时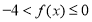 ∴
∴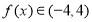 (A:13分)
(A:13分)
③∵当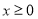 时有
时有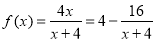 ∴
∴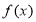 在
在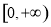 上是增函数,又∵
上是增函数,又∵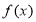 是奇函数∴
是奇函数∴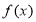 是在
是在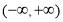 上是增函数,(B:13分)
上是增函数,(B:13分)
∵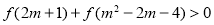 ∴
∴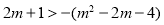 ∴
∴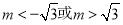
考点:函数的奇偶性及值域,函数的单调性。考查转化思想。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目