题目内容
已知半径为3的圆与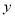
轴相切，圆心在直线
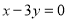上，则此圆的方程为 .
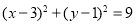或
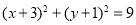
【解析】
试题分析：依题意设圆心为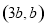
，因为圆与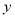
轴相切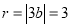，所以
，所以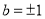
。所以圆的方程为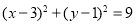或。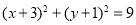
考点：圆的方程的求法。
练习册系列答案
相关题目
题目内容
已知半径为3的圆与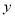轴相切，圆心在直线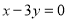上，则此圆的方程为 .
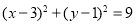或
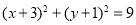
【解析】
试题分析：依题意设圆心为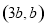，因为圆与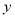轴相切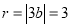，所以，所以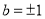。所以圆的方程为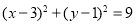或。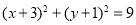
考点：圆的方程的求法。
