题目内容

函数f（x）=|4x-x²|-a有四个零点，则a的取值范围是________．

（0，4）
分析：由题意可得，直线y=a和函数y=|4x-x²|的图象有4个交点，数形结合求得a的取值范围．
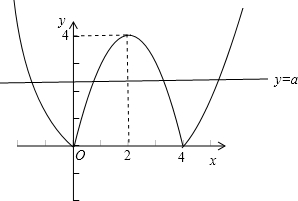
解答：∵函数f（x）=|4x-x²|-a有四个零点，故直线y=a和函数y=|4x-x²|的图象有4个交点，如图所示：
结合图象可得0＜a＜4，
故答案为（0，4）．

点评：本题考查了根的存在性及根的个数判断，以及函数与方程的思想，解答关键是运用数形结合的思想，属于中档题．

练习册系列答案

单元双测全程提优测评卷系列答案

1课3练江苏人民出版社系列答案

尖子生新课堂课时作业系列答案

英才计划同步课时高效训练系列答案

金题1加1系列答案

100分闯关课时作业系列答案

学与练课时作业系列答案

优加学案课时通系列答案

1课1练系列答案

同步训练河北人民出版社系列答案

相关题目

已知函数f（x）=4x-k（x²+2clnx）（c＞1，k∈R）有一个极值点是1．
（I）讨论函数f（x）的单调性；
（II）当c＞1时，记f（x）的极大值为M（c），极小值为N（c），对于t∈R，问函数h(c)=M(c)-

是否存在零点？若存在，请确定零点个数；若不存在，请说明理由．

设函数f（x）=4x+cosx，{a_n}是公差为

的等差数列，f（a₁）+f（a₂）+…+f（a₅）=10π，则[f(a3)]2-a1a5=（　　）

D．无法确定

的定义域为M，函数f（x）=4^x+a•2^x+1+2（x∈M）．
（1）当a=1时，求函数f（x）的值域；
（2）求函数f（x）的最小值．

若A={x∈R|-1≤log

x≤0}，函数f（x）=4^x-3m-2^x+1+5（其中x∈A，m∈R）
（1）求函数f（x）的定义域；
（2）求函数f（x）的最小值．

（文）函数f（x）=4^x的反函数f^-1（x）=