题目内容
若A={x∈R|-1≤log
x≤0},函数f(x)=4x-3m-2x+1+5(其中x∈A,m∈R)
(1)求函数f(x)的定义域;
(2)求函数f(x)的最小值.
| 1 | 3 |
(1)求函数f(x)的定义域;
(2)求函数f(x)的最小值.
分析:(1)由题意可得 log
3≤log
x≤log
1,由此求得x的范围,即可求得函数的定义域.
(2)令 t=2x,(2≤t≤8),则y=t2-6mt+5=(t-3m)2-9m2+5,利用二次函数的性质分类讨论,求得函数f(x)的最小值.
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)令 t=2x,(2≤t≤8),则y=t2-6mt+5=(t-3m)2-9m2+5,利用二次函数的性质分类讨论,求得函数f(x)的最小值.
解答:解:(1)在A中由|-1≤log
x≤0 得 log
3≤log
x≤log
1,…(2分)
∴1≤x≤3,…(4分)
即函数f(x)的定义域为[1,3].…(5分)
(2)函数 y=f(x)=4x-3m-2x+1+5,
令 t=2x,(2≤t≤8),则y=t2-6mt+5=(t-3m)2-9m2+5,…(8分)
若 3m≤2,即 m≤
,则 ymin=f(2)=9-12m.…(9分)
若 2<3m<8,即
<m<
,则 ymin=f(3m)=5-9m2.…(10分)
若 3m≥8,即 m≥
,ymin=f(8)=64-48m+5=69-48m,…(11分)
综上所述,fmin(x)=
.…(13分)
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴1≤x≤3,…(4分)
即函数f(x)的定义域为[1,3].…(5分)
(2)函数 y=f(x)=4x-3m-2x+1+5,
令 t=2x,(2≤t≤8),则y=t2-6mt+5=(t-3m)2-9m2+5,…(8分)
若 3m≤2,即 m≤
| 2 |
| 3 |
若 2<3m<8,即
| 2 |
| 3 |
| 8 |
| 3 |
若 3m≥8,即 m≥
| 8 |
| 3 |
综上所述,fmin(x)=
|
点评:本题主要考查求函数的定义域和值域,对数不等式的解法,二次函数的性质,属于基础题.

练习册系列答案
相关题目
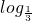 x≤0},函数f(x)=4x-3m-2x+1+5(其中x∈A,m∈R)
x≤0},函数f(x)=4x-3m-2x+1+5(其中x∈A,m∈R)