题目内容
若关于x的方程ax-x-a=0（a＞0）有两个解，则实数a的取值范围为
（1，+∞）
（1，+∞）
．分析：先将关于x的方程ax-x-a=0化成ax=x+a，再画出a＞1和0＜a＜1时的两种函数y=ax，y=x+a的图象，根据图象可直接得出答案．
解答：解：据题意，ax-x-a=0化成ax=x+a，
函数y=ax，的图象与直线y=x+a有两个不同的交点．
①a＞1时：
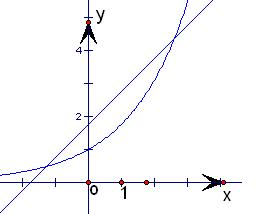
②0＜a＜1时：
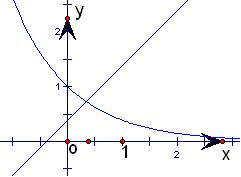
由图知，若关于x的方程ax-x-a=0（a＞0）有两个解，则实数a的取值范围为 （1，+∞）
故答案为：（1，+∞）．
函数y=ax，的图象与直线y=x+a有两个不同的交点．
①a＞1时：
②0＜a＜1时：
由图知，若关于x的方程ax-x-a=0（a＞0）有两个解，则实数a的取值范围为 （1，+∞）
故答案为：（1，+∞）．
点评：本题主要考查指数函数的图象，对于指数函数的图象要分两种情况来考虑，即a＞1和0＜a＜1．属中档题．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
相关题目