题目内容
若关于x的方程|ax-1|-2x=0有两个不相等的实数解,则实数a的取值范围是( )
分析:由方程|ax-1|-2x=0得|ax-1|=2x,分别在坐标系作出函数y=|ax-1|和y=2x的图象,利用两个图象有两个不相等的交点,确定实数a的取值范围.
解答: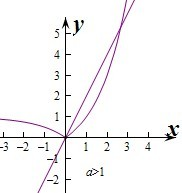 解:由方程|ax-1|-2x=0得|ax-1|=2x,
解:由方程|ax-1|-2x=0得|ax-1|=2x,
设y=|ax-1|和y=2x,
分别在坐标系作出函数y=|ax-1|和y=2x的图象.
①若a>1,则对应图象为上图
此时当x≥0时,y=|ax-1|=ax-1,函数的导数为y'=axlna≥lna,此时函数切线效率的最小值为lna,
∴要使两个图象有两个不相等的交点,则2>lna,即1<a<e2.
②若0<a<1,则对应图象为下图
此时当x≥0时,y=|ax-1|=1-ax,函数的导数为y'=-axlna≤-lna,此时函数切线效率的最大值为-lna,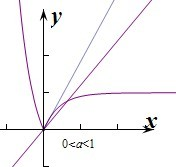
∴要使两个图象有两个不相等的交点,则切线效率-lna>2,即lna<-2,解得0<a<
.
综上实数a的取值范围是1<a<e2或0<a<
.
故选C.
 解:由方程|ax-1|-2x=0得|ax-1|=2x,
解:由方程|ax-1|-2x=0得|ax-1|=2x,设y=|ax-1|和y=2x,
分别在坐标系作出函数y=|ax-1|和y=2x的图象.
①若a>1,则对应图象为上图
此时当x≥0时,y=|ax-1|=ax-1,函数的导数为y'=axlna≥lna,此时函数切线效率的最小值为lna,
∴要使两个图象有两个不相等的交点,则2>lna,即1<a<e2.
②若0<a<1,则对应图象为下图
此时当x≥0时,y=|ax-1|=1-ax,函数的导数为y'=-axlna≤-lna,此时函数切线效率的最大值为-lna,

∴要使两个图象有两个不相等的交点,则切线效率-lna>2,即lna<-2,解得0<a<
| 1 |
| e2 |
综上实数a的取值范围是1<a<e2或0<a<
| 1 |
| e2 |
故选C.
点评:本题主要考查函数零点的应用,利用数形结合是解决此类问题的基本方法,综合性较强,难度较大.

练习册系列答案
相关题目