题目内容
2.已知定义在R上的函数f(x),当x∈[0,1]时,f(x)=x2-x,且对任意的x满足f(x-1)=af(x),a为常数且a≠0,则( )| A. | f(6)<f(6.5) | B. | f(6.5)<f(6) | C. | f(6)<f(7) | D. | f(7)<f(6) |
分析 根据函数的递推关系,求出函数在[6,7]上的单调性,结合一元二次函数的性质进行判断即可.
解答 解:∵对任意的x满足f(x-1)=af(x),a为常数且a≠0,
∴f(x)=$\frac{f(x-1)}{a}$,
若x∈[6,7],
则x-6∈[0,1],
则f(x)=$\frac{f(x-1)}{a}$=$\frac{f(x-2)}{{a}^{2}}=\frac{f(x-3)}{{a}^{3}}=…$=$\frac{f(x-6)}{{a}^{6}}$,
∵当x∈[0,1]时,f(x)=x2-x,
∴f(x)=$\frac{f(x-6)}{{a}^{6}}$=$\frac{(x-6)^{2}-(x-6)}{{a}^{6}}$=$\frac{1}{{a}^{6}}$(x2-13x+42),
则函数的对称轴为x=$\frac{13}{2}$,抛物线开口向上,
则函数在[6,6.5]上单调递减,在[6,5,7]上单调递增,
则f(6.5)<f(6),f(6)=f(7),
故选:B.
点评 本题主要考查函数值的大小比较,根据抽象函数的关系求出函数在[6,7]上的单调性是解决本题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
13.已知点P(x,y)满足$\left\{\begin{array}{l}{x≥1}\\{y≤1}\\{x-y-1≤0}\end{array}\right.$,目标函数z=x+ay(a<0)的最大值与最小值之和为0,则a的值为( )
| A. | -$\frac{3}{2}$ | B. | -2 | C. | -1 | D. | -$\frac{1}{2}$ |
14.执行如图所示的程序框图,若输入x=4,则输出y的值为( )
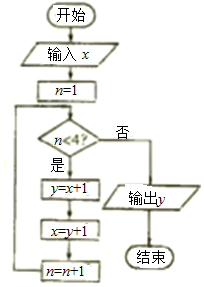

| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
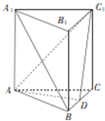 如图,在三棱柱ABC-A1B1C1中,底面ABC为正三角形,CC1⊥平面ABC,AB=AA1,D是BC上的一点,且AD⊥C1D.
如图,在三棱柱ABC-A1B1C1中,底面ABC为正三角形,CC1⊥平面ABC,AB=AA1,D是BC上的一点,且AD⊥C1D.