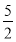题目内容
9.过抛物线C:y2=2px(p>0)的焦点且斜率为2的直线与C交于A、B两点,以AB为直径的圆与C的准线有公共点M,若点M的纵坐标为2,则p的值为( )| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
分析 取AB的中点N,分别过A、B、N作准线的垂线AP、BQ、MN,垂足分别为P、Q、M,作出图形,利用抛物线的定义及梯形的中位线性质可推导,|MN|=$\frac{1}{2}$|AB|,从而可判断圆与准线的位置关系:相切,确定抛物线y2=2px的焦点,设直线AB的方程,与抛物线方程联立,由韦达定理可得AB的中点M的纵坐标为$\frac{p}{2}$,由条件即可得到p=4.
解答 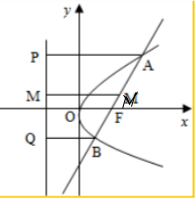 解:取AB的中点N,分别过A、B、N作准线的垂线AP、BQ、MN,
解:取AB的中点N,分别过A、B、N作准线的垂线AP、BQ、MN,
垂足分别为P、Q、M,如图所示:
由抛物线的定义可知,|AP|=|AF|,|BQ|=|BF|,
在直角梯形APQB中,|MN|=$\frac{1}{2}$(|AP|+|BQ|)
=$\frac{1}{2}$(|AF|+|BF|)=$\frac{1}{2}$|AB|,
故圆心N到准线的距离等于半径,
即有以AB为直径的圆与抛物线的准线相切,
由M的纵坐标为2,即N的纵坐标为2,
抛物线y2=2px的焦点坐标为($\frac{p}{2}$,0),
设直线AB的方程为y=2(x-$\frac{p}{2}$),即x=$\frac{1}{2}$y+$\frac{p}{2}$,
与抛物线方程y2=2px联立,消去x,得y2-py-p2=0
由韦达定理可得AB的中点N的纵坐标为$\frac{p}{2}$,
即有p=4,
故选C.
点评 本题考查直线与抛物线的位置关系、直线圆的位置关系,考查抛物线的定义,考查数形结合思想,属中档题.

练习册系列答案
相关题目
20.已知i为虚数单位,复数z=a+bi(a,b∈R)的虚部b记作Im(z),则Im($\frac{1}{1+i}$)=( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
17.在平面直角坐标系中,直线y=$\frac{\sqrt{3}}{3}$x与圆x2+y2-8x+4=0交于A、B两点,则线段AB的长为( )
| A. | 4$\sqrt{2}$ | B. | 4$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
14.若集合A={1,m,m2},集合B={2,4},则“m=-2”是“A∩B={4}”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
1.如图复平面内的点A表示复数z,则复数$\frac{z}{1+i}$表示的点所在的象限为( )


| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.向量$\overrightarrow{a}$与$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{2}$,且$\overrightarrow{a}⊥\overrightarrow{b}$,则|$\overrightarrow{a}+\overrightarrow{b}$|为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{2}$ |
19.已知x,y满足$\left\{\begin{array}{l}{kx-y+2≥0(k<0)}\\{x+y-2≥0}\\{y≥0}\end{array}\right.$,则使目标函数z=y-x取得最小值-4的最优解为( )
| A. | (2,-2) | B. | (-4,0) | C. | (4,0) | D. | (7,3) |
 ,若向量
,若向量 与
与 平行,则
平行,则 ( )
( ) B.
B.
 D.
D.