题目内容
已知A＝{x|ax－1>0}，B＝{x|x2－3x＋2>0}．
(1)若A∩B＝A，求实数a的取值范围；
(2)若A∩∁RB≠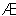
，求实数a的取值范围．
（1）a≤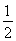
（2）a＞
.
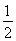【解析】(1)由于A∩B＝A得A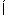
B，由题意知B＝{x|x>2或x<1}．若a>0，则x>
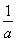≥2，得0＜a≤
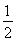；若a＝0，则A＝
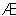，成立；若a＜0，则x＜
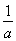＜1，根据数轴可知均成立．综上所述，a≤.
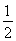(2)∁RB＝{x|1≤x≤2}，若a＝0，则A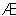＝，不成立；若a＜0，则x＜
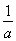＜1，不成立；若a＞0，则x＞
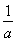，由
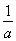＜2得a＞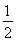
.综上所述，a＞.
练习册系列答案
名牌学校分层周周测系列答案
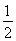黄冈海淀全程培优测试卷系列答案
相关题目
