题目内容
【题目】如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
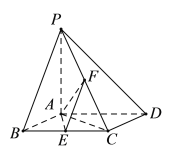
(I)证明:AE⊥PD;
(II)设AB=PA=2,
①求异面直线PB与AD所成角的正弦值;
②求二面角E-AF-C的余弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)①![]() ②
②![]()
【解析】
(Ⅰ)通过![]() 得到
得到![]() ,再证明
,再证明![]() ,
,![]() 平面PAD,然后证明
平面PAD,然后证明![]() ;(Ⅱ)以A为坐标原点,建立如图所示的空间直角坐标系,①求出
;(Ⅱ)以A为坐标原点,建立如图所示的空间直角坐标系,①求出![]() ,
,![]() ,得到异面直线PB与AD所成角的正弦函数值;②求出平面AEF的一法向量,平面AFC的一法向量,利用空间向量的数量积求解所求二面角的余弦值.
,得到异面直线PB与AD所成角的正弦函数值;②求出平面AEF的一法向量,平面AFC的一法向量,利用空间向量的数量积求解所求二面角的余弦值.
(Ⅰ)证明:由四边形![]() 为菱形,
为菱形,![]() ,
,
可得![]() 为正三角形.
为正三角形.
因为![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
又![]() ,因此
,因此![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() .
.
而![]() 平面
平面![]() ,
,![]() 平面
平面![]() 且
且![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() .
.
所以![]()
(Ⅱ)由(Ⅰ)知![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,建立空间直角坐标系,又
为坐标原点,建立空间直角坐标系,又![]() 分别为
分别为![]() 的中点,所以
的中点,所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
①![]() ,.
,.
∴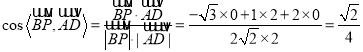 ,
,
设异面直线![]() 与
与![]() 所成角为
所成角为![]() ,∴
,∴![]()
②![]()
设平面![]() 的一法向量为
的一法向量为![]()
则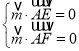 ,因此
,因此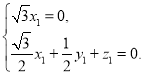
取![]()
因为![]() ,
,![]() ,
,![]() ,
,
所以 ![]() ,
,
故![]() 为平面
为平面![]() 的一法向量.
的一法向量.
又![]() =
=![]() ,
,
所以 ![]() =
=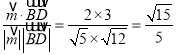 .
.
因为二面角![]() 为锐角,所以所求二面角的余弦值为
为锐角,所以所求二面角的余弦值为![]()

【题目】某工厂生产某种型号的农机具零配件,为了预测今年7月份该型号农机具零配件的市场需求量,以合理安排生产,工厂对本年度1月份至6月份该型号农机具零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的6组数据如下表所示:
(单位:千件)之间的6组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 11.1 | 9.1 | 9.4 | 10.2 | 8.8 | 11.4 |
销售量 | 2.5 | 3.1 | 3 | 2.8 | 3.2 | 2.4 |
(1)根据1至6月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(2)结合(1)中的线性回归方程,假设该型号农机具零配件的生产成本为每件3元,那么工厂如何制定7月份的销售单价,才能使该月利润达到最大?(计算结果精确到0.1)
参考公式:回归直线方程![]() ,
,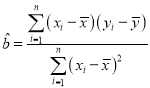
参考数据:![]() ,
,![]()
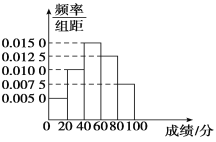
【题目】某中学准备组建“文科”兴趣特长社团,由课外活动小组对高一学生文科、理科进行了问卷调查,问卷共100道题,每题1分,总分100分,该课外活动小组随机抽取了200名学生的问卷成绩(单位:分)进行统计,将数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成5组,绘制的频率分布直方图如图所示,若将不低于60分的称为“文科方向”学生,低于60分的称为“理科方向”学生.
分成5组,绘制的频率分布直方图如图所示,若将不低于60分的称为“文科方向”学生,低于60分的称为“理科方向”学生.
|
|
(1)根据已知条件完成下面![]() 列联表,并据此判断是否有99%的把握认为是否为“文科方向”与性别有关?
列联表,并据此判断是否有99%的把握认为是否为“文科方向”与性别有关?
(2)将频率视为概率,现在从该校高一学生中用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中“文科方向”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列、期望
的分布列、期望![]() 和方差
和方差![]() .
.
参考公式: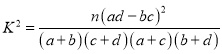 ,其中
,其中![]() .
.
参考临界值:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |