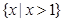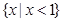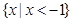题目内容

在极坐标系中，曲线C：p=2cosθ上任意一点P到点Q（
2
，
π
4
）的最大距离等于（　　）
A、
2
B、2
C、
3
D、
6
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：把极坐标方程化为直角坐标方程，可得Q在圆上，可得PQ的最大距离为直径．
解答：解：曲线C的普通方程为（x-1）2+y2=1，Q点直角坐标为（1，1），显然点Q在圆上，
故PQ的最大距离为直径2，
故选：B．
点评：本题主要考查把极坐标方程化为直角坐标方程的方法，属于基础题．
练习册系列答案
相关题目
复数z=
3-i
i
（i为虚数单位），则|z|等于（　　）
A、10
B、
10
C、5
D、
5
如图，四边形ABCD内接于圆O，∠BOD=110°，∠BCD等于（　　）
A、100°B、110°C、125°D、135°
直角坐标系xoy中，点（2，-2）在矩阵M=
0   1
a   0
对应变换作用下得到点（-2，4），曲线C：x2+y2=1在矩阵M对应变换作用下得到曲线C′，
（1）求曲线C′的方程．
（2）求矩阵M的特征值和特征向量．
将正整数1，2，3，4，…，n2（n≥2）任意排成n行n列的数表．对于某一个数表，计算各行和各列中的任意两个数a，b（a＞b）的比值
a
b
，称这些比值中的最小值为这个数表的“特征值”．若aij表示某个n行n列数表中第i行第j列的数（1≤i≤n，1≤j≤n），且满足aij=
i+(j-i-1)n，    i＜j
i+(n-i+j-1)n，  i≥j
，当n=4时数表的“特征值”为
 
．
曲线C：
x=1+cosθ
y=sinθ
（θ为参数）与直线l：
x=-2+
1
2
t
y=1-
1
2
t
（t为参数）的位置关系是（　　）
A、相交B、相离C、相切D、不确定
在直角坐标系xOy中，直线C1的参数方程为C1：
x=1+t
y=-
3
+
3
t
（t为参数）；以O为极点，x轴正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=2．
（1）求曲线C2的直角坐标方程，说明它表示什么曲线，并写出其参数方程；
（2）过直线C1上的点向曲线ρ=1作切线，求切线长的最小值．
已知数列{an}满足a1=1，an+1=an2-2an+1（n∈N*），则a2014=（　　）
A、1B、0C、2014D、-2014
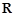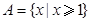已知全集为，集合，那么集合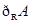等于（   ）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网