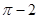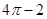题目内容
已知函数 的导函数
的导函数 的图象如图所示,则关于函数
的图象如图所示,则关于函数 ,下列说法正确的是
,下列说法正确的是
A.在 处取得极大值 处取得极大值 |
B.在区间 上是增函数 上是增函数 |
C.在 处取得极大值 处取得极大值 |
D.在区间 上是减函数 上是减函数 |
B
解析试题分析:由导函数 的图象可知:当-1 <x<4时,
的图象可知:当-1 <x<4时,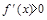 ,此时函数f(x)单调递增,当x<-1或x>4时,
,此时函数f(x)单调递增,当x<-1或x>4时,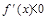 ,此时函数f(x)单调递减,当x=-1或x=4时,
,此时函数f(x)单调递减,当x=-1或x=4时,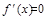 ,∴函数f(x)在
,∴函数f(x)在 处取得极小值,在
处取得极小值,在 处无极值,在区间
处无极值,在区间 上先增加后减少,故选B
上先增加后减少,故选B
考点:本题考查了导数的运用及函数的性质
点评:熟练掌握导数法判断函数单调性的法则及极值的概念是解决此类问题的关键

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
函数 有小于1的极值点,则实数
有小于1的极值点,则实数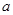 的取值范围是( )
的取值范围是( )
A.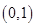 | B.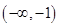 | C. | D.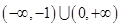 |
三次函数当 时有极大值
时有极大值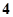 ,当
,当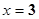 时有极小值
时有极小值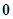 ,且函数过原点,则此函数是( )
,且函数过原点,则此函数是( )
A.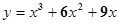 | B.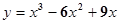 |
C. | D.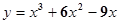 |
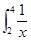 dx等于 ( )
dx等于 ( )
| A.-2ln2 | B.2ln2 | C.-ln2 | D.ln2 |
函数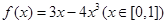 的最大值是( )
的最大值是( )
| A.1 | B.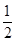 | C.0 | D.-1 |
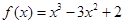 在区间
在区间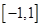 上的最大值是( )
上的最大值是( )
| A.-2 | B.0 | C.2 | D.4 |
设连续函数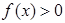 ,则当
,则当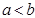 时,定积分
时,定积分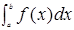 的符号
的符号
| A.一定是正的 |
| B.一定是负的 |
C.当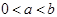 时是正的,当 时是正的,当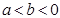 时是负的 时是负的 |
| D.以上结论都不对 |
已知二次函数 的图象如图所示,则它与
的图象如图所示,则它与 轴所围图形的面积为:
轴所围图形的面积为:
A. | B. | C. | D. |
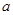 、
、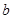 ,则集合
,则集合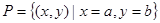 所表示的平面图形面积等于( )
所表示的平面图形面积等于( )