题目内容
己知函数 是定义域为R的奇函数,且
是定义域为R的奇函数,且 ,
, 的导函数
的导函数 的图象如图所示。若正数
的图象如图所示。若正数 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
B
解析试题分析:先由导函数f′(x)是过原点的二次函数入手,再结合f(x)是定义域为R的奇函数求出f(x);然后根据a、b的约束条件画出可行域,最后利用 的几何意义解决问题。解:由f(x)的导函数f′(x)的图象,设f′(x)=mx3,则f(x)=
的几何意义解决问题。解:由f(x)的导函数f′(x)的图象,设f′(x)=mx3,则f(x)=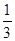 mx3+n.∵f(x)是定义域为R的奇函数,∴f(0)=0,即n=0,因为
mx3+n.∵f(x)是定义域为R的奇函数,∴f(0)=0,即n=0,因为 ,则可知-15m=-1,m=
,则可知-15m=-1,m=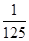 ,故可知由于
,故可知由于 ,即有
,即有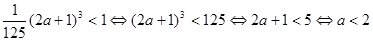 ,求解得到参数a的取值范围,进而得到
,求解得到参数a的取值范围,进而得到 的取值范围是
的取值范围是 ,选B.
,选B.
考点:导数的运用
点评:数形结合是数学的基本思想方法:遇到二元一次不等式组要考虑线性规划,这都是由数到形的转化策略。同时能结合不等式的性质来求解范围,属于基础题。

练习册系列答案
相关题目
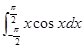 的值为 ( )
的值为 ( )
| A.0 | B.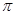 | C.2 | D.-2 |
已知 =
= ·
·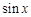 ,则
,则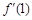 =( )
=( )
A.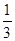 + cos1 + cos1 | B.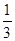 sin1+cos1 sin1+cos1 | C.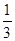 sin1-cos1 sin1-cos1 | D.sin1+cos1 |
三次函数当 时有极大值
时有极大值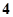 ,当
,当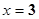 时有极小值
时有极小值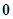 ,且函数过原点,则此函数是( )
,且函数过原点,则此函数是( )
A.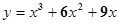 | B.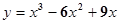 |
C. | D.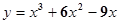 |
曲线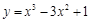 在点
在点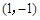 处的切线方程为
处的切线方程为
A.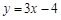 | B.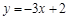 | C.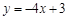 | D.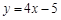 |
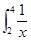 dx等于 ( )
dx等于 ( )
| A.-2ln2 | B.2ln2 | C.-ln2 | D.ln2 |
函数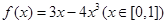 的最大值是( )
的最大值是( )
| A.1 | B.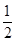 | C.0 | D.-1 |
设连续函数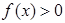 ,则当
,则当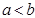 时,定积分
时,定积分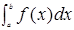 的符号
的符号
| A.一定是正的 |
| B.一定是负的 |
C.当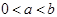 时是正的,当 时是正的,当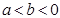 时是负的 时是负的 |
| D.以上结论都不对 |
已知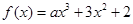 ,若
,若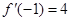 ,则
,则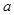 的值等于( )
的值等于( )
A.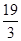 | B.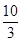 | C.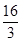 | D. |