题目内容
把一颗骰子投掷两次,观察掷出的点数,并记第一次掷出的点数为 ,第二次掷出的点数为
,第二次掷出的点数为 .试就方程组
.试就方程组 (※)解答下列问题:
(※)解答下列问题:
(1)求方程组没有解的概率;
(2)求以方程组(※)的解为坐标的点落在第四象限的概率..
(1)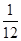 ;(2)
;(2)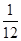
解析试题分析:(1)由方程组 没解,即相对应的两条直线平行,所以可求得
没解,即相对应的两条直线平行,所以可求得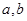 的关系式,再列举
的关系式,再列举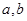 的符合情况的个数,由于总的基本事件的个数为36.即可得结论.
的符合情况的个数,由于总的基本事件的个数为36.即可得结论.
(2)由方程组 的解为坐标的点落在第四象,即将解出该方程组的解,由方程组的解对应一个点,根据点落在第四象限的坐标特点,即可得到
的解为坐标的点落在第四象,即将解出该方程组的解,由方程组的解对应一个点,根据点落在第四象限的坐标特点,即可得到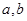 的关系式,从而列举符合
的关系式,从而列举符合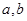 关系的情况的个数.再根据古典概型的概念得到结论.
关系的情况的个数.再根据古典概型的概念得到结论.
(1)由题意知,总的样本空间有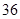 组 1分
组 1分
方法1:若方程没有解,则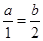 ,即
,即 3分
3分
(方法2:带入消元得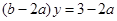 ,因为
,因为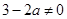 ,所以当
,所以当  时方程组无解)
时方程组无解)
所以符合条件的数组为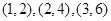 , 4分
, 4分
所以 ,故方程组没有解的概率为
,故方程组没有解的概率为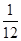 5分
5分
(2)由方程组 得
得 6分
6分
若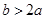 ,则有
,则有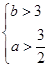 即
即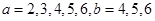 符合条件的数组有
符合条件的数组有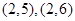 共有
共有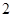 个 8分
个 8分
若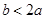 ,则有
,则有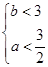 即
即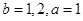 符合条件的数组有
符合条件的数组有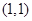 共
共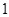 个 10分
个 10分
∴所以概率为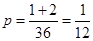 ,
,
即点P落在第四象限且P的坐标满足方程组(※)的概率为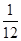 . 12分
. 12分
考点:1.两直线的位置关系.2.古典概型.3.列举归纳的数学思想.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
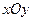 中, 二元一次方程
中, 二元一次方程 (
( 不同时为
不同时为 )表示过原点的直线. 类比以上结论有: 在空间直角坐标系
)表示过原点的直线. 类比以上结论有: 在空间直角坐标系 中, 三元一次方程
中, 三元一次方程 (
( 不同时为
不同时为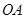 ,规划建一座新桥
,规划建一座新桥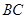 ,同时设立一个圆形保护区,规划要求,新桥
,同时设立一个圆形保护区,规划要求,新桥 垂直;保护区的边界为圆心
垂直;保护区的边界为圆心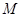 在线段
在线段 和
和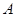 到该圆上任一点的距离均不少于80
到该圆上任一点的距离均不少于80 ,经测量,点
,经测量,点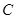 位于点
位于点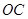 为河岸),
为河岸),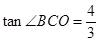 .
.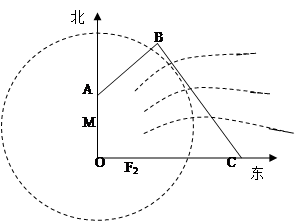
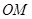 多长时,圆形保护区的面积最大?
多长时,圆形保护区的面积最大?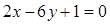 并且与曲线
并且与曲线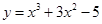 相切的直线方程.
相切的直线方程.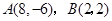 .
.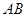 的中垂线方程;
的中垂线方程;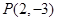 点且与直线
点且与直线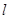 的方程;
的方程;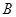 点射向(2)中的直线
点射向(2)中的直线 ,求反射光线所在的直线方程.
,求反射光线所在的直线方程.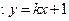 与两点
与两点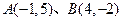 ,若直线l与线段AB相交,则实数k的取值范围是 .
,若直线l与线段AB相交,则实数k的取值范围是 . ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.
