题目内容
如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.
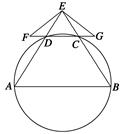
(1)证明:CD∥AB;
(2)延长CD到F,延长DC到G,使得EF=EG,证明:A,B,G,F四点共圆.
【答案】
(1)证明同位角相等。CD∥AB.
(2)证得∠AFG+∠GBA=180°.说明A,B,G,F四点共圆.
【解析】
试题分析: (1)因为EC=ED,所以∠EDC=∠ECD.
因为A,B,C,D四点在同一圆上,所以∠EDC=∠EBA.
故∠ECD=∠EBA.
所以CD∥AB.
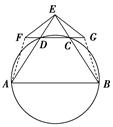
(2)由(1)知,AE=BE.因为EF=EG,故∠EFD=∠EGC,从而∠FED=∠GEC.
连结AF,BG,则△EFA≌△EGB,故∠FAE=∠GBE.
又CD∥AB,∠EDC=∠ECD,所以∠FAB=∠GBA.
所以∠AFG+∠GBA=180°.
故A,B,G,F四点共圆.
考点:本题主要考查圆的切割线定理,三角形全等。
点评:中档题,涉及圆的问题,往往与三角形相关联,利用三角形相似或三角形全等解决问题。

练习册系列答案
相关题目
 12、如图,A,B,C,D四点都在平面a,b外,它们在a内的射影A1,B1,C1,D1是平行四边形的四个顶点,在b内的射影A2,B2,C2,D2在一条直线上,求证:ABCD是平行四边形.
12、如图,A,B,C,D四点都在平面a,b外,它们在a内的射影A1,B1,C1,D1是平行四边形的四个顶点,在b内的射影A2,B2,C2,D2在一条直线上,求证:ABCD是平行四边形. 如图,A,B,C,D为空间四点,在△ABC中,
如图,A,B,C,D为空间四点,在△ABC中, 如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC=
如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC= 如图,A、B、C、D是某煤矿的四个采煤点,l是公路,图中所标线段为道路,ABQP、BCRQ、CDSR近似于正方形.已知A、B、C、D四个采煤点每天的采煤量之比约为5:1:2:3,运煤的费用与运煤的路程、所运煤的重量都成正比.现要从P、Q、R、S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在( )
如图,A、B、C、D是某煤矿的四个采煤点,l是公路,图中所标线段为道路,ABQP、BCRQ、CDSR近似于正方形.已知A、B、C、D四个采煤点每天的采煤量之比约为5:1:2:3,运煤的费用与运煤的路程、所运煤的重量都成正比.现要从P、Q、R、S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在( ) (2013•房山区二模)如图,A,B,C,D是⊙O上的四个点,过点B的切线与DC的延长线交于点E.若∠BCD=110°,则∠DBE=( )
(2013•房山区二模)如图,A,B,C,D是⊙O上的四个点,过点B的切线与DC的延长线交于点E.若∠BCD=110°,则∠DBE=( )