Question

如图，A，B，C，D为空间四点，在△ABC中，AB=2，AC=BC=

2

．等边三角形ADB以AB为轴运动．当CD=

 

时，面ACD⊥面ADB．

Answer 1

分析：取出AB中点E，连接DE，CE，由等边三角形ADB可得出DE⊥AB，又平面ADB⊥平面ABC，故DE⊥平面ABC，在Rt△DEC中用勾股定理求出CD

解答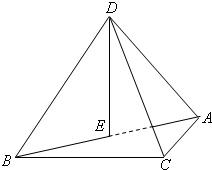：解：取AB的中点E，连接DE，CE，
因为ADB是等边三角形，所以DE⊥AB．
当平面ADB⊥平面ABC时，
因为平面ADB∩平面ABC=AB，
所以DE⊥平面ABC，
可知DE⊥CE
由已知可得 DE=

3

，EC=1，在Rt△DEC中，CD=

DE2+EC2

=2．
故答案为2

点评：本题考查的知识点是面面垂直的性质及空间两点间的位置关系，其中根据已知条件得到DE⊥CE将空间两点间的距离问题转化为解直角三角形问题是解答本题的关键．