Question

【题目】已知，

（1）判断的奇偶性并说明理由；（2）求证：函数在上是增函数；

（3）若，求实数的取值范围。

Answer 1

【答案】（1）奇函数（2）详见解析（3）

【解析】

试题分析：（1）判断函数奇偶性首先判断定义域是否对称，再判断的关系，从而确定函数奇偶性；（2）证明函数单调性一般采用定义法，首先假设，通过判断的正负号确定函数的单调性；（3）借助于单调性与奇偶性将不等式化简为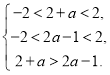，解不等式可得到实数的取值范围

试题解析：（1）奇函数

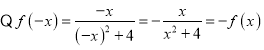，所以函数是奇函数 ……5分

（2）证明：设，为区间上的任意两个值，且

= ……8分

因为 所以 即

所以函数在上是增函数 …………………10分

（3）解：因为为奇函数

所以由得

因为函数在上是增函数

所以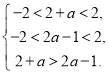 …13分 即 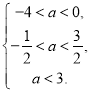故 ……15分