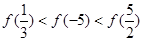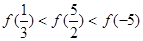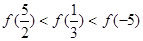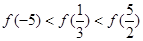题目内容
已知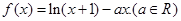
Ⅰ.求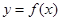 的单调区间;
的单调区间;
Ⅱ.当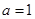 时,求
时,求 在定义域上的最大值;
在定义域上的最大值;
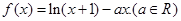
Ⅰ.求
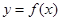 的单调区间;
的单调区间;Ⅱ.当
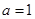 时,求
时,求 在定义域上的最大值;
在定义域上的最大值;(Ⅰ)①当a = 0时,  的单调递增区间为
的单调递增区间为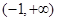
②当a < 0 时, 的单调递增区间为
的单调递增区间为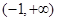
③当a > 0时, 的单调递增区间为
的单调递增区间为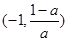 ,单调递减区间为
,单调递减区间为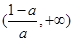 。
。
(Ⅱ) 的最大值是0
的最大值是0
 的单调递增区间为
的单调递增区间为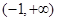
②当a < 0 时,
 的单调递增区间为
的单调递增区间为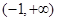
③当a > 0时,
 的单调递增区间为
的单调递增区间为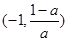 ,单调递减区间为
,单调递减区间为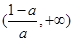 。
。(Ⅱ)
 的最大值是0
的最大值是0(I)先确定函数f(x)的定义域,然后再利用导数大(小)于零,分别求出其单调增区间或减区间.
(II)当a=1时,在(I)的基础上可知其单调性,进而可求出其最值.
解:(Ⅰ)定义域为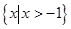 ,
,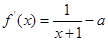 ———————————
———————————
①当a = 0时,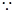
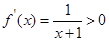 ,
,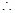
 的单调递增区间为
的单调递增区间为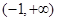 —
—
②当a < 0 时,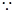
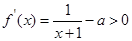
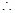
 的单调递增区间为
的单调递增区间为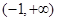
③当a > 0时,由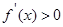 ,则
,则 ,所以
,所以 的单调递增区间为
的单调递增区间为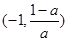 ,
,
由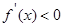 ,则
,则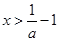 ,所以
,所以 的单调递减区间为
的单调递减区间为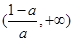
(Ⅱ)当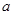 = 1时,
= 1时, ,
,
由(Ⅰ)可知 在
在 上单调递增,在
上单调递增,在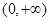 上单调递减,所以
上单调递减,所以
 的最大值是0
的最大值是0
(II)当a=1时,在(I)的基础上可知其单调性,进而可求出其最值.
解:(Ⅰ)定义域为
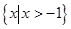 ,
,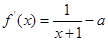 ———————————
———————————①当a = 0时,
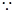
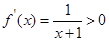 ,
,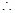
 的单调递增区间为
的单调递增区间为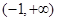 —
—②当a < 0 时,
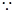
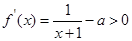
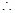
 的单调递增区间为
的单调递增区间为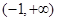
③当a > 0时,由
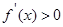 ,则
,则 ,所以
,所以 的单调递增区间为
的单调递增区间为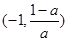 ,
,由
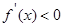 ,则
,则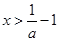 ,所以
,所以 的单调递减区间为
的单调递减区间为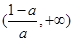
(Ⅱ)当
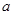 = 1时,
= 1时, ,
,由(Ⅰ)可知
 在
在 上单调递增,在
上单调递增,在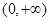 上单调递减,所以
上单调递减,所以 的最大值是0
的最大值是0
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
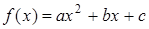 中
中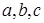 均为实数,且满足
均为实数,且满足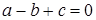 ,对于任意实数
,对于任意实数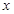 都有
都有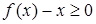 ,并且当
,并且当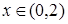 时有
时有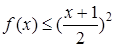 成立。
成立。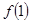 的值;
的值; 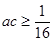 ;
; 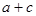 取最小值时,函数
取最小值时,函数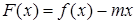 (
(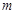 为实数)是单调函数,求证:
为实数)是单调函数,求证: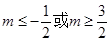 。
。 为同一函数的是( ).
为同一函数的是( ).



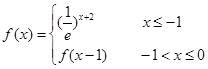 , 若f (x)≥x+a“对于任意x∈R恒成立,则常数a的取值范围是( )
, 若f (x)≥x+a“对于任意x∈R恒成立,则常数a的取值范围是( )
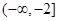
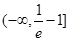
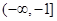
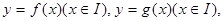 若对于任意
若对于任意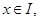 存在
存在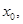 使得
使得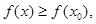
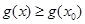 且
且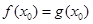 ,则称
,则称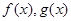 为“兄弟函数”.已知
为“兄弟函数”.已知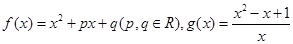 是定义在区间
是定义在区间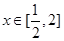 上的“兄弟函数”,那么函数
上的“兄弟函数”,那么函数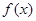 在区间
在区间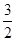
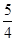
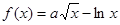
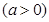
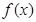 在
在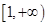 上递增,求
上递增,求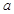 的取值范围;
的取值范围;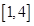 上的最小值.
上的最小值. ,若
,若 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的 ,总有
,总有 ,则实数
,则实数 的取值范围是( )
的取值范围是( )



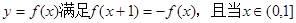 时单调递增,
时单调递增,