题目内容
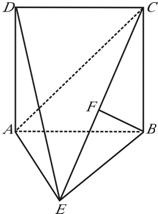 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.(1)求证:AE⊥平面BCE;
(2)求三棱锥E-ABC的体积.
分析:(1)欲证AE⊥平面BCE,由题设条件知可先证BF⊥AE,CB⊥AE,再结合线面垂直的判定定理得出线面垂直即可;
(2)由题设,底面三角形ACD的面积不难求出,关键是高的求法,可以过点E作EO⊥AB交AB于点O,再求得OE的长度,最后用锥体体积公式可求出三棱锥E-ABC的体积.
(2)由题设,底面三角形ACD的面积不难求出,关键是高的求法,可以过点E作EO⊥AB交AB于点O,再求得OE的长度,最后用锥体体积公式可求出三棱锥E-ABC的体积.
解答:解:(1)∵BF⊥平面ACE.∴BF⊥AE
∵二面角D-AB-E为直二面角.且CB⊥AB.
∴CB⊥平面ABE∴CB⊥AE
∵BF∩CB=B
∴AE⊥平面BCE
(2)过点E作EO⊥AB交AB于点O,OE=1
∵二面角D-AB-E为直二面角,
∴EO⊥平面ABCD
∴VE-ACD=
S△ACD•EO=
•
•AD•DC•EO=
∵二面角D-AB-E为直二面角.且CB⊥AB.
∴CB⊥平面ABE∴CB⊥AE
∵BF∩CB=B
∴AE⊥平面BCE
(2)过点E作EO⊥AB交AB于点O,OE=1
∵二面角D-AB-E为直二面角,
∴EO⊥平面ABCD
∴VE-ACD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
点评:本题考查了用线面垂直的判定定理证明线面垂直,以及用二面角的定义求二面角,求棱锥的体积,本题涉及到的知识与技巧较多,综合性较强,在解题过程中要注意体会问题的转化方向,及解决方法.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
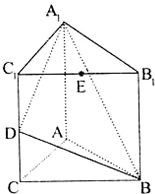 直三棱柱A1B1C1-ABC的三视图如图所示,D、E分别为棱CC1和B1C1的中点.
直三棱柱A1B1C1-ABC的三视图如图所示,D、E分别为棱CC1和B1C1的中点.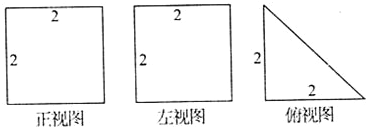
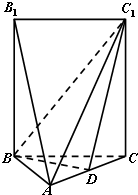 如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.
如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.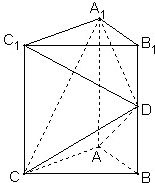 如图,直三棱柱ABC-A1B1C1中,
如图,直三棱柱ABC-A1B1C1中, 如图:五面体A-BCC1B1中,AB1=4,△ABC 是正三角形,AB=2,四边形 BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.
如图:五面体A-BCC1B1中,AB1=4,△ABC 是正三角形,AB=2,四边形 BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点. 如图,直四棱柱A1B1C1D1-ABCD的高为3,底面是边长为4,且∠DAB=60°的菱形,O是AC与BD的交点,O1是A1C1与B1D1的交点.
如图,直四棱柱A1B1C1D1-ABCD的高为3,底面是边长为4,且∠DAB=60°的菱形,O是AC与BD的交点,O1是A1C1与B1D1的交点.