题目内容
 如图:五面体A-BCC1B1中,AB1=4,△ABC 是正三角形,AB=2,四边形 BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.
如图:五面体A-BCC1B1中,AB1=4,△ABC 是正三角形,AB=2,四边形 BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.(1)求证:AB1∥平面BDC1;
(2)求二面角C-BC1-D的大小;
(3)若A、B、C、C1为某一个球面上的四点,求该球的半径r.
分析:(1)连接B1C交BC1于O,连接DO,由三角形的中位线性质可得 DO∥AB1,从而证明AB1∥平面BDC1.
(2)过点D作DN⊥BC于点N,过点N作HH⊥BC1,连接DH,则易知∠DHN为二面角C-BC1-D的平面角,分别求出DN,NH的长,即可得二面角C-BC1-D的大小;
(3)取AC1的中点M,连接DM,则DM∥CC1.以DA、DB、DM所在直线分别为x轴、y轴、z轴建立空间直角坐标系D-xyz,则可求球的半径.
(2)过点D作DN⊥BC于点N,过点N作HH⊥BC1,连接DH,则易知∠DHN为二面角C-BC1-D的平面角,分别求出DN,NH的长,即可得二面角C-BC1-D的大小;
(3)取AC1的中点M,连接DM,则DM∥CC1.以DA、DB、DM所在直线分别为x轴、y轴、z轴建立空间直角坐标系D-xyz,则可求球的半径.
解答: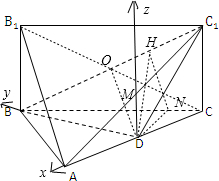 (1)证明:连接B1C交BC1于点O,则O为B1C中点,连接OD,
(1)证明:连接B1C交BC1于点O,则O为B1C中点,连接OD,
则在△B1AC中,AB1∥OD.
∵OD?平面BDC1,AB1?平面BDC1.
∴AB1∥平面BDC1.…(3分)
(2)过点D作DN⊥BC于点N,则
∵二面角A-BC-C1为直二面角
∴DN⊥平面CBC1.
过点N作HH⊥BC1,连接DH,则由三垂线定理知DH⊥BC1.
∴∠DHN为二面角C-BC1-D的平面角.…(4分)
∵DN=DC•sin60°=
,
∴CN=
,BN=
.…(5分)
∵△ABB1为直角三角形,
∴CC1=BB1=2
,
∴BC1=4.…(6分)
∵Rt△BNH~Rt△BC1C
∴
=
,
∴HN=
.…(7分)
∴tan∠DHN=
=
=
,
∴二面角C-BC1-D的大小为arctan
.…(8分)
(3)取AC1的中点M,连接DM,则DM∥CC1.
以DA、DB、DM所在直线分别为x轴、y轴、z轴建立空间直角坐标系D-xyz(如图所示).…(9分)
则A(1,0,0),C1(-1,0,2
),
设球心为点O,O到平面ABC的距离为h,则O(0,
,h).…(10分)
∵OC1=OA=r,
∴
=
,
∴h=
,
∴r=
=
.…(12分)
 (1)证明:连接B1C交BC1于点O,则O为B1C中点,连接OD,
(1)证明:连接B1C交BC1于点O,则O为B1C中点,连接OD,则在△B1AC中,AB1∥OD.
∵OD?平面BDC1,AB1?平面BDC1.
∴AB1∥平面BDC1.…(3分)
(2)过点D作DN⊥BC于点N,则
∵二面角A-BC-C1为直二面角
∴DN⊥平面CBC1.
过点N作HH⊥BC1,连接DH,则由三垂线定理知DH⊥BC1.
∴∠DHN为二面角C-BC1-D的平面角.…(4分)
∵DN=DC•sin60°=
| ||
| 2 |
∴CN=
| 1 |
| 2 |
| 3 |
| 2 |
∵△ABB1为直角三角形,
∴CC1=BB1=2
| 3 |
∴BC1=4.…(6分)
∵Rt△BNH~Rt△BC1C
∴
| BN |
| BC1 |
| NH |
| CC1 |
∴HN=
3
| ||
| 4 |
∴tan∠DHN=
| DN |
| NH |
| ||||
|
| 2 |
| 3 |
∴二面角C-BC1-D的大小为arctan
| 2 |
| 3 |
(3)取AC1的中点M,连接DM,则DM∥CC1.
以DA、DB、DM所在直线分别为x轴、y轴、z轴建立空间直角坐标系D-xyz(如图所示).…(9分)
则A(1,0,0),C1(-1,0,2
| 3 |
设球心为点O,O到平面ABC的距离为h,则O(0,
| ||
| 3 |
∵OC1=OA=r,
∴
1+
|
1+
|
∴h=
| 3 |
∴r=
1+
|
| ||
| 3 |
点评:本题以多面体为载体,考查线面平行,考查面面角,考查利用空间向量解决立体几何问题,解题的关键是利用线线平行证明线面平行,正确作出二面角的平面角.

练习册系列答案
相关题目
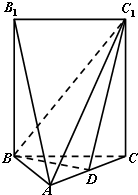 如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.
如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.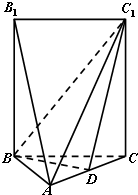 如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.
如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.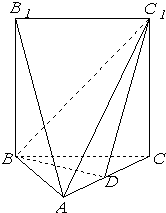 如图,五面体A-BCC1B1中,AB1=4,底面ABC是正三角形,AB=2,四边形BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.
如图,五面体A-BCC1B1中,AB1=4,底面ABC是正三角形,AB=2,四边形BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.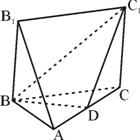 (1)求证:AB1∥面BDC1;(2)求二面角C-BC1-D的大小;
(1)求证:AB1∥面BDC1;(2)求二面角C-BC1-D的大小;