题目内容
已知sinα和cosα是方程4x2+2| 6 |
(1)求m的值;
(2)求
| sinα |
| 1-cotα |
| cosα |
| 1-tanα |
分析:(1)由已知中sinθ、cosθ是关于x的方程4x2+2
x+m=0的两个实根,我们根据方程存在实根的条件,我们可以求出满足条件的m的值,然后根据韦达定理结合同角三角函数关系,我们易求出满足条件的m的值.
(2)
+
=
+
=
=sinα+cosα,由此能求出其结果.
| 6 |
(2)
| sinα |
| 1-cotα |
| cosα |
| 1-tanα |
| sinα | ||
1-
|
| cosα | ||
1-
|
| sin2α-cos 2α |
| sinα-cosα |
解答:解:(1)sina+cosa=-
,
sina•cosa=
,
由sin2a+cos2a=1=(sina+cosa)2-2sinacosa=
-
=1
∴m=1.
(2)
+
=
+
=
=sinα+cosα
=-
.
| ||
| 2 |
sina•cosa=
| m |
| 4 |
由sin2a+cos2a=1=(sina+cosa)2-2sinacosa=
| 6 |
| 4 |
| 2m |
| 4 |
∴m=1.
(2)
| sinα |
| 1-cotα |
| cosα |
| 1-tanα |
=
| sinα | ||
1-
|
| cosα | ||
1-
|
=
| sin2α-cos 2α |
| sinα-cosα |
=sinα+cosα
=-
| ||
| 2 |
点评:本题考查二次函数的性质和弦切互化,解题时要认真审题,注意韦达定理的合理运用和三角函数的相互转化.

练习册系列答案
相关题目
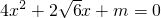 的两实根
的两实根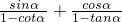 的值.
的值.