题目内容
已知sinα和cosα是方程8x2+6mx+2m+1=0的两个实根,则m的值等于 .
【答案】分析:因为sinα和cosα是方程8x2+6mx+2m+1=0的两个实根,所以根据韦达定理用m表示出sinα+cosα及sinαcosα,利用同角三角函数间的基本关系得出关系式,把表示出的sinα+cosα及sinαcosα代入得到关于m的方程,求出方程的解可得m的值.
解答:解:由题意,根据韦达定理得:sinα+cosα=-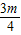 ,sinαcosα=
,sinαcosα=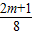 ,
,
∵sin2α+cos2α=1,
∴sin2α+cos2α=(sinα+cosα)2-2sinαcosα=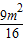 -
-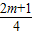 =1,
=1,
即9m2-8m-20=0,
因式分解得:(9m+10)(m-2)=0,
解得:m1=-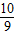 ,m2=2,
,m2=2,
把m=2代入原方程得:8x2+12x+5=0,∵△=144-160=-16<0,方程无解,故舍去,
则m的值为-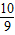 .
.
故答案为:-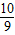
点评:此题考查了同角三角函数间的基本关系的运用,韦达定理及根的判别式的应用,灵活运用韦达定理及同角三角函数间的基本关系得出关于m的方程是解本题的关键.
解答:解:由题意,根据韦达定理得:sinα+cosα=-
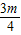 ,sinαcosα=
,sinαcosα=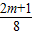 ,
,∵sin2α+cos2α=1,
∴sin2α+cos2α=(sinα+cosα)2-2sinαcosα=
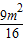 -
-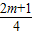 =1,
=1,即9m2-8m-20=0,
因式分解得:(9m+10)(m-2)=0,
解得:m1=-
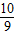 ,m2=2,
,m2=2,把m=2代入原方程得:8x2+12x+5=0,∵△=144-160=-16<0,方程无解,故舍去,
则m的值为-
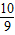 .
.故答案为:-
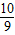
点评:此题考查了同角三角函数间的基本关系的运用,韦达定理及根的判别式的应用,灵活运用韦达定理及同角三角函数间的基本关系得出关于m的方程是解本题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
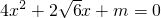 的两实根
的两实根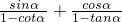 的值.
的值.