题目内容
对于定义在集合D上的函数y=f(x),若f(x)在D上具有单调性,且存在区间[a,b]⊆D(其中a<b),使当x∈[a,b]时,f(x)的值域是[a,b],则称函数f(x)是D上的正函数,区间[a,b]称为f(x)的“等域区间”.
(1)已知函数
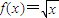 是[0,+∞)上的正函数,试求f(x)的等域区间.
是[0,+∞)上的正函数,试求f(x)的等域区间.(2)试探究是否存在实数k,使函数g(x)=x2+k是(-∞,0)上的正函数?若存在,求出k的取值范围;若不存在,请说明理由.
【答案】分析:(1)因为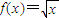 在[0,+∞)上是增函数,所以当x∈[a,b],f(x)的值域是[f(a),f(b)],由此能求出f(x)的等域区间.
在[0,+∞)上是增函数,所以当x∈[a,b],f(x)的值域是[f(a),f(b)],由此能求出f(x)的等域区间.
(2)设存在实数k,使函数g(x)=x2+k是(-∞,0)上为减函数.当x∈[a,b]时,g(x)的值域是[g(a),g(b)],若函数g(x)=x2+k是(-∞,0)上的正函数,则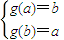 .由此能够导出存在实数
.由此能够导出存在实数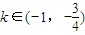 ,使函数g(x)=x2+k是(-∞,0)上的正函数.
,使函数g(x)=x2+k是(-∞,0)上的正函数.
解答:解:(1)因为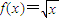 在[0,+∞)上是增函数
在[0,+∞)上是增函数
所以当x∈[a,b],f(x)的值域是[f(a),f(b)],
又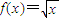 是[0,+∞)上的正函数
是[0,+∞)上的正函数
∴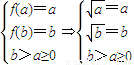 ,
,
∴a=0,b=1,
∴f(x)的等域区间为[0,1].…(4分)
(2)设存在实数k,使函数g(x)=x2+k是(-∞,0)上为减函数.
∴当x∈[a,b]时,g(x)的值域是[g(a),g(b)],
若函数g(x)=x2+k是(-∞,0)上的正函数,
则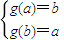 ,
,
即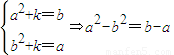 ,
,
∵a≠b,∴a+b=-1即b=-a-1,
∵a<b<0即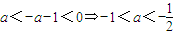 …(8分)
…(8分)
∴关于a的方程a2+a+k+1=0在区间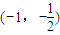 内有实根,
内有实根,
由a2+a+k+1=0得k+1=-a2-a…(10分),
∵函数y=-a2-a在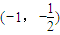 上为增函数,
上为增函数,
∴当a∈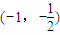 时,
时,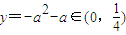 …(12分)
…(12分)
∴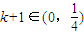 即
即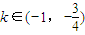
故存在实数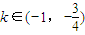 使函数g(x)=x2+k是(-∞,0)上的正函数…(14分)
使函数g(x)=x2+k是(-∞,0)上的正函数…(14分)
点评:本题考查函数恒成立的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.
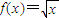 在[0,+∞)上是增函数,所以当x∈[a,b],f(x)的值域是[f(a),f(b)],由此能求出f(x)的等域区间.
在[0,+∞)上是增函数,所以当x∈[a,b],f(x)的值域是[f(a),f(b)],由此能求出f(x)的等域区间.(2)设存在实数k,使函数g(x)=x2+k是(-∞,0)上为减函数.当x∈[a,b]时,g(x)的值域是[g(a),g(b)],若函数g(x)=x2+k是(-∞,0)上的正函数,则
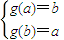 .由此能够导出存在实数
.由此能够导出存在实数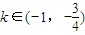 ,使函数g(x)=x2+k是(-∞,0)上的正函数.
,使函数g(x)=x2+k是(-∞,0)上的正函数.解答:解:(1)因为
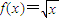 在[0,+∞)上是增函数
在[0,+∞)上是增函数所以当x∈[a,b],f(x)的值域是[f(a),f(b)],
又
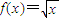 是[0,+∞)上的正函数
是[0,+∞)上的正函数∴
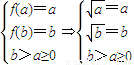 ,
,∴a=0,b=1,
∴f(x)的等域区间为[0,1].…(4分)
(2)设存在实数k,使函数g(x)=x2+k是(-∞,0)上为减函数.
∴当x∈[a,b]时,g(x)的值域是[g(a),g(b)],
若函数g(x)=x2+k是(-∞,0)上的正函数,
则
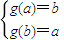 ,
,即
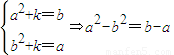 ,
,∵a≠b,∴a+b=-1即b=-a-1,
∵a<b<0即
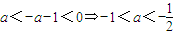 …(8分)
…(8分)∴关于a的方程a2+a+k+1=0在区间
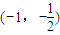 内有实根,
内有实根,由a2+a+k+1=0得k+1=-a2-a…(10分),
∵函数y=-a2-a在
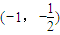 上为增函数,
上为增函数,∴当a∈
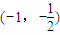 时,
时,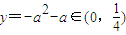 …(12分)
…(12分)∴
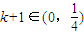 即
即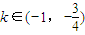
故存在实数
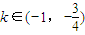 使函数g(x)=x2+k是(-∞,0)上的正函数…(14分)
使函数g(x)=x2+k是(-∞,0)上的正函数…(14分)点评:本题考查函数恒成立的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
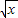 是[0,+∞)上的正函数,则f(x)的等域区间为 .
是[0,+∞)上的正函数,则f(x)的等域区间为 .