题目内容
对于定义在集合D上的函数y=f(x),若f(x)在D上具有单调性且存在区间[a,b]⊆D(其中a<b)使当x∈[a,b]时,f(x)的值域是[a,b],则称函数f(x)是D上的“正函数”,区间[a,b]称为f(x)的“等域区间”.
(1)已知函数f(x)=x3是正函数,试求f(x)的所有等域区间;
(2)若g(x)=
+k是正函数,试求实数k的取值范围;
(3)是否存在实数a,b(a<b<1)使得函数f(x)=|1-
|是[a,b]上的“正函数”?若存在,求出区间[a,b],若不存在,说明理由.
(1)已知函数f(x)=x3是正函数,试求f(x)的所有等域区间;
(2)若g(x)=
| x+2 |
(3)是否存在实数a,b(a<b<1)使得函数f(x)=|1-
| 1 |
| x |
分析:(1)根据导数符号可知f(x)=x3在R上是增函数,则x∈[a,b]时,f(x)的值域为[a3,b3],最后根据f(x)=x3是正函数建立等式关系,解之即可求出所求;
(2)g(x)=
+k在[-2,+∞)上是增函数,则x∈[a,b]时,f(x)的值域为[g(a),g(b)],根据g(x)=
+k是正函数,建立等式关系,即k=(
)2-
-2有两个不等的实根,数形结合即可求出k的范围;
(3)假设存在区间[a,b],使得x∈[a,b]时,H(x)=|1-
|的值域为[a,b],讨论当a<b<0时与当0<a<b<1时是否存在实数a、b即可.
(2)g(x)=
| x+2 |
| x+2 |
| x+2 |
| x+2 |
(3)假设存在区间[a,b],使得x∈[a,b]时,H(x)=|1-
| 1 |
| x |
解答:解:(1)∵f′(x)=3x2≥0
∴f(x)=x3在R上是增函数
则x∈[a,b]时,f(x)的值域为[a3,b3]
又f(x)=x3是正函数
∴
解得
或
或
故f(x)的等域区间有三个:[0,1],[-1,0],[-1,1]…(5分)
(2)∵g(x)=
+k在[-2,+∞)上是增函数
∴x∈[a,b]时,f(x)的值域为[g(a),g(b)]
若g(x)=
+k是正函数,则有
即
故方程x=
+k有两个不等的实根.…(7分)
即k=(
)2-
-2有两个不等的实根
令
=t≥0,h(t)=t2-t-2=(t-
)2-
(t≥0)
数形结合知:k∈(-
,-2]…(9分)
(3)假设存在区间[a,b],使得x∈[a,b]时,H(x)=|1-
|的值域为[a,b],又0∉[a,b]故ab>0
当a<b<0时,H(x)=1-
在[a,b]上单增.
∴
⇒a,b是方程x=1-
的两负根
又方程x2-x+1=0无解
故此时不存在…(11分)
当0<a<b<1时,H(x)=
-1在[a,b]上单减
∴
⇒
⇒a=b,又a<b
故此时不存在…(13分)
综上可知:不存在实数a<b<1使得f(x)的定义域和值域均为[a,b]…(14分)
∴f(x)=x3在R上是增函数
则x∈[a,b]时,f(x)的值域为[a3,b3]
又f(x)=x3是正函数
∴
|
|
|
|
故f(x)的等域区间有三个:[0,1],[-1,0],[-1,1]…(5分)
(2)∵g(x)=
| x+2 |
∴x∈[a,b]时,f(x)的值域为[g(a),g(b)]
若g(x)=
| x+2 |
|
|
故方程x=
| x+2 |
即k=(
| x+2 |
| x+2 |
令
| x+2 |
| 1 |
| 2 |
| 9 |
| 4 |
数形结合知:k∈(-
| 9 |
| 4 |
(3)假设存在区间[a,b],使得x∈[a,b]时,H(x)=|1-
| 1 |
| x |
当a<b<0时,H(x)=1-
| 1 |
| x |
∴
|
| 1 |
| x |
又方程x2-x+1=0无解
故此时不存在…(11分)
当0<a<b<1时,H(x)=
| 1 |
| x |
∴
|
|
故此时不存在…(13分)
综上可知:不存在实数a<b<1使得f(x)的定义域和值域均为[a,b]…(14分)
点评:本题主要考查了函数值域的求解,以及利用函数的单调性求函数的值域,同时考查了分类讨论的思想,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
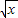 是[0,+∞)上的正函数,则f(x)的等域区间为 .
是[0,+∞)上的正函数,则f(x)的等域区间为 .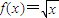 是[0,+∞)上的正函数,试求f(x)的等域区间.
是[0,+∞)上的正函数,试求f(x)的等域区间.