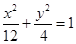题目内容
设双曲线 的两条渐近线与直线
的两条渐近线与直线 分别交于A,B两点,F为该双曲线的右焦点.若
分别交于A,B两点,F为该双曲线的右焦点.若 , 则该双曲线的离心率的取值范围是( )
, 则该双曲线的离心率的取值范围是( )
A. | B.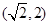 | C. | D. |
B
解析试题分析:由题可得又曲线的渐近线方程为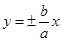 ,与
,与 交于
交于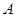 ,
,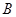 两点,联立可得坐标,不妨令
两点,联立可得坐标,不妨令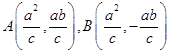 ,则
,则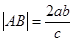 ,又右焦点
,又右焦点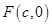 ,故
,故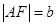 ,
,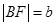 ,在
,在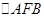 中,
中, ,即
,即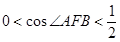 ,由余弦定理
,由余弦定理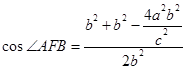 ,可化为
,可化为 ,又
,又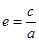 ,故可得
,故可得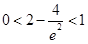 ,解得
,解得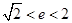 .
.
考点:双曲线的几何性质,余弦定理.

练习册系列答案
相关题目
如果方程 表示双曲线,则实数
表示双曲线,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
设 ,
,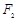 分别是椭圆
分别是椭圆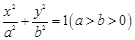 的左、右焦点,过
的左、右焦点,过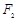 的直线交椭圆于
的直线交椭圆于 ,
, 两点,若
两点,若 ,
, ,则椭圆的离心率为( )
,则椭圆的离心率为( )
A. | B. | C. | D. |
已知P是双曲线 的右支上一点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,下列命题正确的是( ).
的右支上一点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,下列命题正确的是( ).
A.双曲线的焦点到渐近线的距离为 ; ; |
B.若 ,则e的最大值为 ,则e的最大值为 ; ; |
| C.△PF1F2的内切圆的圆心的横坐标为a ; |
D.若∠F1PF2的外角平分线交x轴与M, 则 . . |
设抛物线x2=4y与椭圆 +
+ =1交于点E,F,则△OEF(O为坐标原点)的面积为( )
=1交于点E,F,则△OEF(O为坐标原点)的面积为( )
A.3 | B.4 | C.6 | D.12 |
设抛物线y2=2px(p>0)的焦点为F,点A在y轴上,若线段FA的中点B在抛物线上,且点B到抛物线准线的距离为 ,则点A的坐标为( )
,则点A的坐标为( )
| A.(0,±2) | B.(0,2) |
| C.(0,±4) | D.(0,4) |
已知双曲线 -
- =1的右焦点为(3,0),则该双曲线的离心率等于( )
=1的右焦点为(3,0),则该双曲线的离心率等于( )
A. | B. | C. | D.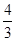 |
设e是椭圆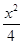 +
+ =1的离心率,且e∈(
=1的离心率,且e∈( ,1),则实数k的取值范围是( )
,1),则实数k的取值范围是( )
| A.(0,3) | B.(3, ) ) |
C.(0,3)∪( ,+∞) ,+∞) | D.(0,2) |

 的左、右焦点为
的左、右焦点为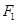 、
、 ,离心率为
,离心率为 ,过
,过 交C于A、B两点,若
交C于A、B两点,若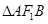 的周长为
的周长为 ,则C的方程为
,则C的方程为 B.
B. C.
C. D.
D.