题目内容
若 与
与 在区间
在区间 上都是减函数,则a的取值范围是()
上都是减函数,则a的取值范围是()
A. B.
B. C.
C.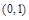 D.
D.
8.求下列函数的零点,可以采用二分法的是( B )
A.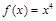 B.
B.
C. D.
D.
 与
与 在区间
在区间 上都是减函数,则a的取值范围是()
上都是减函数,则a的取值范围是()A.
 B.
B. C.
C.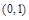 D.
D.
8.求下列函数的零点,可以采用二分法的是( B )
A.
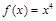 B.
B.
C.
 D.
D.
D
f(x)是开口向下的二次函数,所以在对称轴右侧为减函数,又因为f(x)在区间[1,2]上是减函数,所以区间[1,2]为函减区间的子区间,通过比较函数的单调减区间与区间[1,2]的端点的大小,可求出a的一个范围,因为g(x)是反比例函数通过左右平移得到的,所以当a大于0时,在(-∞,-1)和(-1,+∞)都为减函数,当a小于0时,在(-∞,-1)和(-1,+∞)都为增函数,这样,有得到a的一个范围,两个范围求公共部分,即得a的值范围.
解:∵函数f(x)=-x2+2ax的对称轴为x=a,开口向下,
∴单调间区间为[a,+∞)
又∵f(x)在区间[1,2]上是减函数,
∴a≤1
∵g(x)= 在区间[1,2]上是减函数,
在区间[1,2]上是减函数,
∴a>0
综上得0<a≤1
故答案为D
解:∵函数f(x)=-x2+2ax的对称轴为x=a,开口向下,
∴单调间区间为[a,+∞)
又∵f(x)在区间[1,2]上是减函数,
∴a≤1
∵g(x)=
 在区间[1,2]上是减函数,
在区间[1,2]上是减函数,∴a>0
综上得0<a≤1
故答案为D

练习册系列答案
相关题目
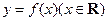 的图象过点(0,-3),且
的图象过点(0,-3),且 的解集
的解集 .
. 的解析式;
的解析式; 的最值.
的最值.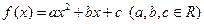 满足下列条件:
满足下列条件: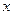 ∈R时,
∈R时,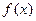 的最小值为0,且f (
的最小值为0,且f (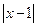 +1恒成立。
+1恒成立。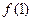 的值;
的值; 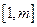 时,就有
时,就有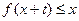 成立。
成立。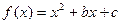 和
和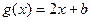 ,若对任意的
,若对任意的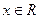 ,恒有
,恒有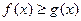
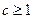 且
且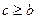
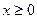 时,
时,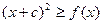
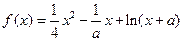 ,其中常数
,其中常数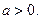
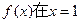 处取得极值,求a的值;
处取得极值,求a的值;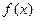 的单调递增区间;
的单调递增区间;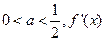 表示
表示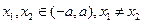 ,
,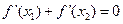 ,试比较
,试比较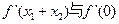 的大小,
的大小, 并加以证明。
并加以证明。 +4x+3(x∈R),那么函数f(x)的最小值为____.
+4x+3(x∈R),那么函数f(x)的最小值为____. +c的图象的开口向下,对称轴为x=1,方程 ax2+bx+c=0的两个解一个在区间(2,3)中,则下列判断正确的是
+c的图象的开口向下,对称轴为x=1,方程 ax2+bx+c=0的两个解一个在区间(2,3)中,则下列判断正确的是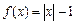 ,关于
,关于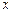 的方程
的方程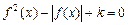 ,若方程恰有8个不同的实根,则实数k的取值范围是 .
,若方程恰有8个不同的实根,则实数k的取值范围是 .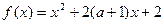 在区间
在区间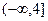 上是减函数,则实数
上是减函数,则实数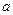 的取值范围是
的取值范围是


