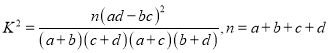题目内容
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,经过点
,经过点![]() 的直线与椭圆相交于
的直线与椭圆相交于![]() 两点,已知
两点,已知![]() 的周长为
的周长为![]() 。
。
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,求直线
,求直线![]() 的方程。
的方程。
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:
(1)由![]() 可得
可得![]() ,由
,由![]() 的周长为
的周长为![]() 可得
可得![]() ,求得
,求得![]() 可得椭圆的方程。(2)由题意设直线方程为
可得椭圆的方程。(2)由题意设直线方程为![]() ,代入椭圆方程消去x后得到方程
,代入椭圆方程消去x后得到方程![]() ,由根与系数的关系可得
,由根与系数的关系可得![]() ,又由
,又由![]() 得
得![]() ,从而可得
,从而可得![]() 。求得点D的坐标后可得所求的直线方程。
。求得点D的坐标后可得所求的直线方程。
试题解析:
(1)由题意得![]() ,所以
,所以![]() 。
。
又因为![]() ,所以
,所以![]() 。
。
所以![]() 。
。
故椭圆![]() 的方程为
的方程为![]() 。
。
(2)设![]() ,由
,由![]() ,可得
,可得![]() 。
。
又直线![]() 经过点
经过点![]() ,可设直线
,可设直线![]() 的方程为
的方程为![]() ,
,
由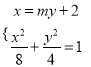 消去x整理得
消去x整理得
![]() ,
,
![]() 。
。
且![]() ,①
,①
又![]() ,②
,②
由①②消去![]() 得
得![]() ,
,
解得![]() 。
。
当![]() 时,可得
时,可得![]() ,故
,故![]() ,此时点D的坐标为
,此时点D的坐标为![]() ,
,
故直线AD的方程为![]() 。
。
当![]() 时,可得
时,可得![]() ,故
,故![]() ,此时点D的坐标为
,此时点D的坐标为![]() ,
,
故直线AD的方程为![]() 。
。
综上可得直线![]() 的方程为
的方程为![]() 。
。

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】微信支付诞生于微信红包,早期知识作为社交的一部分“发红包”而诞生的,在发红包之余才发现,原来微信支付不仅可以用来发红包,还可以用来支付,现在微信支付被越来越多的人们所接受,现从某市市民中随机抽取300为对是否使用微信支付进行调查,得到下列![]() 的列联表:
的列联表:
年轻人 | 非年轻人 | 总计 | |
经常使用微信支付 | 165 | 225 | |
不常使用微信支付 | |||
合计 | 90 | 300 |
根据表中数据,我们得到的统计学的结论是:由__________的把握认为“使用微信支付与年龄有关”。
|
|
|
|
|
|
|
|
|
|
|
|
其中