题目内容
已知a,b,c为实数,且a+b+c+2-2m=0,a2+ b2+
b2+ c2+m-1=0.
c2+m-1=0.
(1)求证:a2+ b2+
b2+ c2≥
c2≥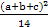 .
.
(2)求实数m的取值范围.
(1)见解析 (2) - ≤m≤1
≤m≤1
解析

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
题目内容
已知a,b,c为实数,且a+b+c+2-2m=0,a2+ b2+
b2+ c2+m-1=0.
c2+m-1=0.
(1)求证:a2+ b2+
b2+ c2≥
c2≥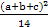 .
.
(2)求实数m的取值范围.
(1)见解析 (2) - ≤m≤1
≤m≤1
解析

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案